Спектральное представление колебаний: периодических, непериодические колебания

Спектральное представление колебаний

Спектральное представление периодических колебаний

При формировании и обработке сигналов часто приходится иметь дело с колебаниями, описываемыми периодическими функциями вида S(t) = S(t±kT), где k = 1, 2, …; ? — период (рис. 2.9).

Зададим на отрезке полную систему тригонометрических ортогональных функций:

где ?1 = 2? / T — основная частота.

Выбор такого базиса наиболее распространен, так как в результате его использования обеспечиваются:
• сравнительная простота формирования гармонических колебаний;
• инвариантность сигналов относительно их преобразований в линейных электрических цепях (ЛЭЦ). При прохождении через ЛЭЦ изменяются только амплитуда и начальная фаза составляющих.

В этом случае для сигнала S(t) обобщенный ряд Фурье будет иметь вид
Здесь коэффициенты разложения
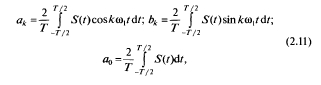откуда видно, что периодический сигнал содержит постоянную составляющую и бесконечный набор гармонических колебаний с частотами (Формула), которые являются кратными основной частоте.

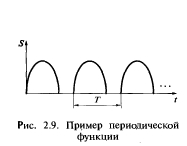
Рис. 2.9. Пример периодической функции

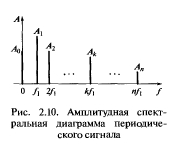
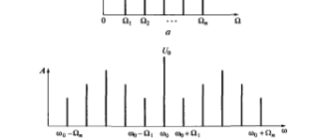
Рис. 2.10. Амплитудная спектральная диаграмма периодического сигнала

Представим коэффициенты разложения в виде
где Ак — амплитуда; фк — начальная фаза.

Тогда ряд Фурье можно записать в другой эквивалентной форме:
Выражение (2.12) можно интерпретировать графически как сумму гармоник с частотами, кратными основной частоте f1 = 1 / T , амплитудами Аk и начальными фазами ?k. При этом различают амплитудный и фазовый спектры.

Амплитудный спектр показан на рис. 2.10.

Рассмотрим теперь комплексную форму записи сигнала в виде ряда Фурье. В этом случае в качестве базисных функций применяются комплексные экспоненты:

где k = 0, ±1, ±2, …; j — мнимая единица.

Такая система также является полной.

Соответственно обобщенный ряд Фурье, известный как ряд Фурье в комплексной форме, приобретает следующий вид:
Здесь комплексная амплитуда k-й гармоники
связана с Аk, ?k, bk, ?k следующими выражениями:
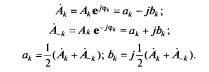Из этих выражений следует, что фазовый угол ?k является нечетной функцией относительно k, т. е. относительно частоты, а модуль комплексной амплитуды Аk — четной.

Как видно из соотношения (2.13), суммирование распространено на положительные (k) и отрицательные (–k) частоты. Последние имеют фиктивный характер. Действительную составляющую (Формула) сигнала с частотой (Формула) получают как сумму двух комплексных функций:
т. е. происходит взаимное уничтожение мнимых частей.

Отметим также, что спектр периодического сигнала является дискретным и бесконечным. С увеличением периода следования сигналов разность частот между соседними гармониками уменьшается, т. е. спектр сгущается.

Из формул (2.11) и (2.14) видно, что изменение периода T сказывается на значении амплитуд спектральных составляющих: с увеличением ? амплитуды уменьшаются. Однако форма спектра амплитуд при этом сохраняется.

Пример 2.3. Определим спектр периодической последовательности прямоугольных импульсов с амплитудой Е, длительностью (Формула) и периодом следования Т.

Итак, пусть
По формуле (2.14) находим
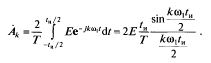Комплексная амплитуда (Формула) пропорциональна функции вида (Формула) и содержит только вещественную часть, т. е.
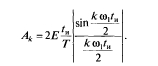Начальные фазы гармоник следующие: ? = 0, в интервалах частот (Формула), где n = 0, 2, 4, …

?k = ±? в интервалах частот (Формула), n = 1, 3, 5, …

С учетом этих соотношений ряд Фурье (2.13) для последовательности прямоугольных импульсов можно записать в виде
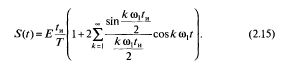Пример 2.4. Периодическая последовательность двухполярных импульсов ±Е задана в виде
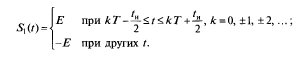Представим S1(t) как результат суммирования однополярных импульсов с амплитудой 2Е и постоянной составляющей –Е, т. е. получим выражение
S1(t) = 2S(t) – E.

Подставив в это выражение S1(t) в виде (2.15), получим ряд Фурье для S1(t):
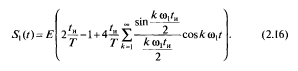Спектральное представление непериодических колебаний

Рассмотренные ранее периодические сигналы на практике почти не встречаются. В подавляющем большинстве случаев в теории и технике связи приходится иметь дело с сигналами и помехами, которые по существу являются непериодическими и к которым аппарат рядов Фурье не применим. Поэтому вместо них используют интегралы Фурье. Такое представление получают посредством перехода от ряда Фурье при стремлении периода повторения сигнала к бесконечности, т.е. T -> ? или f1 = 1 / T = ?1 / (2?) -> 0.

Рассмотрим вновь ряд Фурье в экспоненциальной форме:
где ?? = ?1 = [k?1 – (k – 1)?1] — разность между частотами соседних гармоник, k = 1, 2, …

Определим комплексную спектральную плотность в виде

При ?? -> 0 интервалы между соседними гармониками неограниченно сокращаются, поэтому сумму можно заменить интегралом:
Для нахождения комплексной спектральной плотности S(j?), или комплексного спектра, можно использовать выражение

которое следует из формулы (2.14) для комплексной амплитуды и отличается от нее только наличием множителя 2 / Т.

Выражения (2.17) и (2.18) имеют фундаментальное значение в ТЭС. Первое из них называется “обратным преобразованием Фурье” для сигнала S(t), или “операцией синтеза”, поскольку с его помощью сигнал восстанавливается (синтезируется) из спектральных составляющих. Второе выражение называется “прямым преобразованием Фурье”, или “операцией анализа” сигнала на основе определения его спектральных составляющих. В символической записи соответствие между сигналом S(t) и его преобразованием Фурье S(j?) отображается следующим образом: S(t) ? S(j?).

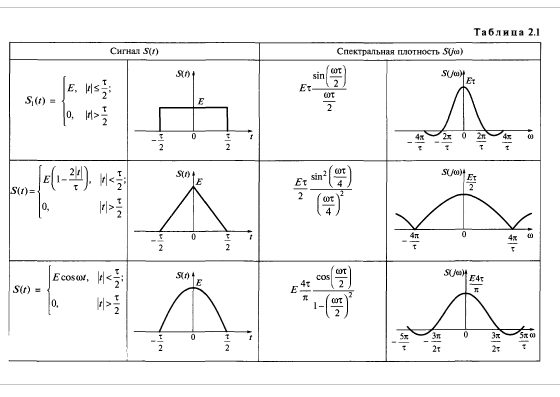
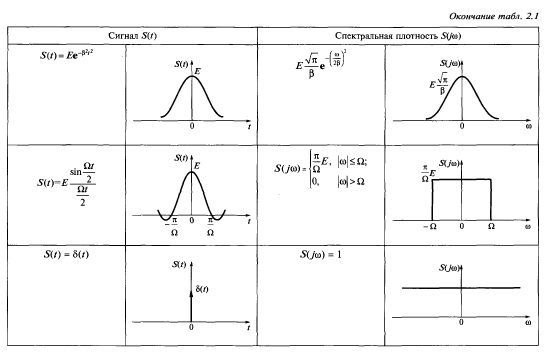
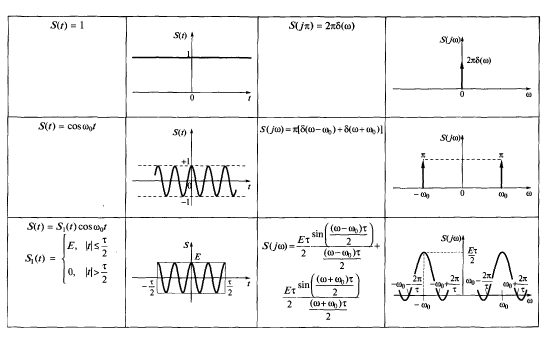
Таблица 2.1.

С учетом четности модуля S(?) и нечетности фазы ?(?) обратное преобразование Фурье (2.17) можно записать в виде.

В соответствии с выражением (2.17) и последней формулой непериодическое колебание S(t) можно рассматривать как сумму комплексных экспоненциальных составляющих или сумму гармонических составляющих , частоты которых располагаются бесконечно близко друг к другу. На основании этого можно говорить о непрерывном, или сплошном, спектре непериодического колебания.

Бесконечно малые амплитуды составляющих определяются выражением Am = с|S(j?)|d?, где (Формула) для формулы (2.17) или с учетом четности модуля S(?), т.е. |S(j?)| отражает спектральную (частотную) плотность амплитуд составляющих. Другими словами, |S(j?)| — это амплитуда, отнесенная к бесконечно малой полосе частот d?.

Особенностью комплексного спектра является его распространение как в положительной, так и в отрицательной области частот. Следовательно, двум составляющим частот ? и –? со спектральной плотностью комплексного спектра соответствует одна гармоническая составляющая частоты ? со спектральной плотностью |S(j?)|.

Сопоставив формулы (2.18) и (2.14) для непериодического колебания и периодического колебания, полученного из исходного непериодического сигнала посредством его периодического продолжения, можно сделать вывод о том, что спектры таких колебаний совпадают по форме и отличаются лишь масштабом.

В табл. 2.1 приведены результаты расчетов S(j?) для колебаний (импульсов) различной формы.