Методы аппроксимации характеристик нелинейных преобразователей сигналов: кусочно-линейная, полиномиальная

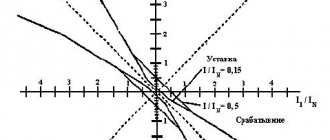
Общие сведения аппроксимации характеристик

Ранее отмечалось, что нелинейный преобразователь может быть описан с помощью вольт-амперной характеристики, которую, как правило, получают экспериментальным путем и затем представляют в виде графической зависимости тока от напряжения. Однако использовать вольт-амперную характеристику в графической форме неудобно. Поэтому возникает задача аппроксимации, под которой понимают приближенное представление нелинейной характеристики математическими методами.

Аппроксимирующая функция должна удовлетворять следующим требованиям:

• быть простой, но допускать последующую математическую обработку;
• достаточно точно отображать экспериментально полученную характеристику.

Исходя из указанных требований в ТЭС применяются следующие методы аппроксимации вольт-амперных характеристик:

• полиномиальная (степенная);
• кусочно-линейная;
• аппроксимация трансцендентными функциями (экспоненциальными, тригонометрическими и др.).

Полиномиальная аппроксимация

Данный метод аппроксимации удобно применять при рассмотрении принципов действия многих нелинейных преобразователей: модуляторов, демодуляторов, генераторов и других при воздействии на них одного либо нескольких гармонических колебаний.

Степенная аппроксимация заключается в записи вольт-амперной характеристики i = f(u) в виде полинома (многочлена) n-й степени:
(Формула).

С помощью такого полинома можно произвести аппроксимацию с любой степенью точности. При этом точность будет выше, если использовать полиномы высоких порядков. Однако это неудобно для анализа.

На практике применяют следующие полиномы:

• первой степени (k = 1) (рис. 3.1)
  
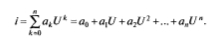
• второй степени (k = 2)
  
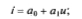
•  укороченный полином третьей степени (k = 3, a2 = 0)
• 
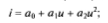
• укороченный полином пятой степени (k = 5, a2 = a4 = 0)
• 

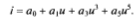
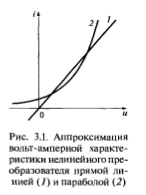
Рис. 3.1. Аппроксимация вольт-амперной характеристики нелинейного преобразователя прямой линией (1) и параболой (2)

Отметим, что аппроксимация многочленом первой степени, которая приводит к получению прямой линии 1 (см. рис. 3.1), не позволяет изучать нелинейные преобразования, например перенос спектра сигнала на другую частоту. Данный вид аппроксимации применяется только при изучении линейных процессов, например усиления. Полином второй степени (квадратичная парабола 2) уже позволяет изучать нелинейные процессы, но только при воздействии слабых сигналов.

В общем случае для использования степенной аппроксимации необходимо знать коэффициенты (Формула) полинома, которые обычно определяют с помощью “метода выбранных точек”. Иными словами, коэффициенты (Формула) находят из условия равенства значений ординат аппроксимированной и действительной характеристик в выбранных точках.

Для аппроксимации полинома n-й степени в пределах интервала ?U, задаваемого диапазоном изменения напряжения u, выбирают n+1 значений напряжения (Формула) и определяют значения токов

В простейшем случае значения (Формула) находят делением интервала ?U на n равных частей ?, как показано на рис. 3.2. При n = 4 значение ? = (u5 – u1) / 4. Далее составляется следующая система уравнений:

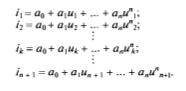
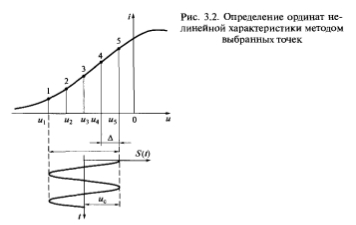
Рис. 3.2. Определение ординат нелинейной характеристики методом выбранных точек

Решение данной системы уравнений определяют коэффициенты (Формула). Если значение u = 0 располагается внутри интервала аппроксимации ?U, то коэффициент a0 находят как значение тока при u = 0.

При вычислении коэффициентов (Формула) иногда предъявляется дополнительное требование равенства не только ординат действительной и аппроксимированной характеристик, но и их производных.

Следует иметь в виду, что аппроксимированная характеристика может резко отличаться от действительной за пределами интервала аппроксимации ?U. Поэтому степенная аппроксимация широко применяется при анализе работы нелинейных устройств, на которые поступают относительно небольшие сигналы. Использовать этот метод при больших отклонениях мгновенных значений входного сигнала от рабочей точки нецелесообразно по причине ухудшения точности.

Кусочно-линейная аппроксимация

Данный метод основан на приближенной замене реальной плавно изменяющейся вольт-амперной характеристики i = f(u) отрезками прямых линий с различными наклонами.

На рис. 3.3 показана аппроксимированная характеристика, содержащая два линейных участка.

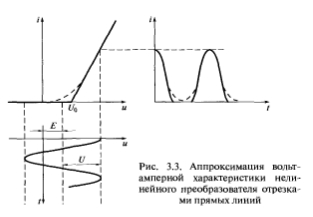
Рис. 3.3. Аппроксимация вольт-амперной характеристики нелинейного преобразователя отрезками прямых линий

Математически эту аппроксимированную характеристику можно записать в виде
(Формула),
где U0 — напряжение отсечки; S — крутизна характеристики, имеющая размерность проводимости (См или А / В).

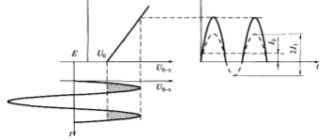
На рис. 3.3 методом проекций построены импульсы тока, получаемые при воздействии гармонического колебания с большой амплитудой. При разложении импульсов в ряд Фурье постоянная составляющая и амплитуды нескольких первых гармоник также близки друг к другу. Иными словами, при больших сигналах кусочно-линейная аппроксимация дает достаточную точность расчетов. При малых сигналах точность падает, и результаты могут быть неверными.

Таким образом, метод кусочно-линейной аппроксимации обычно применяется при анализе процессов нелинейных преобразований в случае больших амплитуд входных сигналов.

Аппроксимация трансцендентными функциями

В данном методе в качестве аппроксимирующих функций используются экспоненты либо их суммы (но не более чем из двух слагаемых), гиперболические, тригонометрические и некоторые другие функции. Чаще всего применяется показательная аппроксимация. Так, в частности, характеристику полупроводникового диода можно аппроксимировать экспонентой:

где (Формула) — обратный ток насыщения; ? — постоянная, характеризующая температурный потенциал.

Данное выражение хорошо определяет начальный участок характеристики. Иными словами, показательная аппроксимация достаточно точна при небольших амплитудах входных сигналов. В противном случае погрешность расчетов оказывается значительной.

Для определения пригодности этого метода аппроксимации для расчета применяют так называемое приведение к линейному виду, сущность которого заключается в следующем. Сначала представленное ранее выражение для тока i логарифмируется:

Далее по реальной вольт-амперной характеристике строится зависимость

Затем в диапазоне напряжений ?U проверяется степень отличия этой характеристики от прямой линии. Если это отличие оказывается небольшим, то исходную характеристику нелинейного элемента (полупроводникового диода) можно аппроксимировать экспонентой.

Нелинейные зависимости более сложного вида можно аппроксимировать суммой двух трансцендентных функций. Например, характеристика туннельного диода описывается выражением
в котором первое слагаемое определяет туннельный ток, а второе — диффузионный.

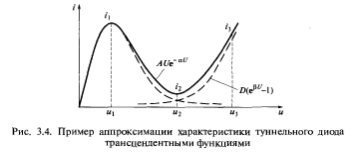
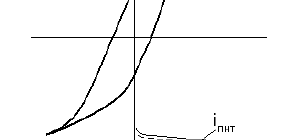
Рис. 3.4. Пример аппроксимации характеристики туннельного диода трансцендентными функциями

Графическое изображение этой характеристики приведено на рис. 3.4, где сплошной линией показан суммарный ток, а штриховой — его компоненты.