onetwoclick.ruЭлементы функциональных пространств
В ТЭС при решении задач возникают, в первую очередь, следующие вопросы.
- Какой величиной можно охарактеризовать сигнал?
- Каким образом любой сигнал можно представить в виде совокупности более простых элементов?
- Как сравнивать между собой разные сигналы?
Эти и многие другие вопросы можно решить с помощью методов функционального анализа, основанных на использовании понятия пространств с различными свойствами.
В современной математике пространство (П) определяется как множество каких-либо объектов, называемых его точками (это могут быть векторы, функции, состояния физической системы, геометрические фигуры и т.д.), причем между этими точками заданы некоторые соотношения, определяющие геометрию пространства. В соответствии с этими соотношениями различают линейные, метрические и нормированные пространства. Существуют также пространства, обладающие сразу несколькими свойствами. Например, евклидово пространство Rn представляет собой линейное метрическое пространство с размерностью n, где элементами являются векторы, и норма вводится через скалярное произведение этих векторов.
Дадим определения линейного пространства (ЛП), метрики и нормы.
Обозначим х, у, z точки или элементы пространства:
1) (Формула) — векторы (действительные или комплексные);
2) x = x(t), y = y(t), z = z(t), — функции (действительные или комплексные);
3) другие элементы.
“Линейным” (L) называется пространство, в котором выполняются следующие правила сложения элементов и умножения их на скаляр ?.
А. Для любых х, у ? L однозначно определяется третий элемент, принадлежащий этому же пространству z ? L и называемый суммой x и у, для которого справедливы следующие условия:
1) х + у = у + х — коммутативность;
2) x + (у + z) = (х + у) + z — ассоциативность;
3) x + 0 = x для всех x ? L, где 0 — нулевой элемент;
4) x + (–х) = 1 для всех x ? L, где x — противоположный элемент, 1 — единичный элемент.
Б. Имеется множество элементов, называемых скалярами, и введена операция, называемая умножением на скаляр, при которой для любого ? и любого x ? L определен элемент ?x ? L, при этом:
1) ?(?x) = (??)x;
2) 1x = x;
3) (? + ?)? – ах + ??;
4) а(х + у) = ах + ау.
Например, прямая линия или совокупность действительных чисел с обычными арифметическими операциями сложения и умножения представляют собой линейное пространство R1, а множество всех аналоговых сигналов, отличных от нуля в интервале времени от t1 до t2 и равных нулю вне этого интервала, — линейное пространство L2.
Линейное пространство, как и обычное трехмерное пространство, имеет некоторую систему координат (СК). В качестве СК используется конечная или бесконечная совокупность элементов — векторов или функций {х1, х2, …, xn}, принадлежащих пространству L и являющихся линейно независимым координатным базисом, т.е. базисом, для которого равенство (Формула) возможно лишь в случае, если все (Формула). Это равенство означает, что в линейно независимом множестве элемент является линейной комбинацией других элементов.
Рис. 2.6. Разложение вектора на составляющие в трехмерном пространстве
Любой элемент линейного пространства можно представить в виде разложения по координатному базису (Формула):
(2.1) — проекции элемента x относительно выбранного базиса.
В случае когда элементами пространства являются векторы (действительные или комплексные), разложение (2.1) имеет вид
Если же элементы линейного пространства представляют собой функции (действительные или комплексные), выражение (2.1) будет иметь вид
Число n называется размерностью линейного пространства. Любое множество n линейно независимых векторов в ЛП может служить его базисом, следовательно, ЛП имеет не один базис.
Например, вектор в обычном трехмерном пространстве можно записать следующим образом:
где x1, x2, x3 — проекции вектора (Формула) на оси координат, называемые его координатами; 
— взаимно-перпендикулярные единичные векторы (координатный базис, орты или оси координат);
— составляющие вектора (Формула) (рис. 2.6).
Следующей ступенью в усовершенствовании структуры пространства является установление расстояния между его элементами, которое также называется “метрикой”. Иными словами, каждой паре элементов пространства ставится в соответствие положительное число, которое трактуется как расстояние между элементами. В качестве расстояния используется функционал d(x, у) = R — метрика, обладающая следующими свойствами:
1) d(x, у) >= 0 и d(x, у) = 0 только в случае, если x = у;
2) d(x, у) = d(y, x) — симметрия;
3) d(x, у) < d(x, z) + d(z, у) — неравенство треугольника.
Эти свойства интуитивно понятны, так как известно:
- расстояние — это неотрицательная величина;
- расстояние от x до у равно расстоянию от у до х;
- длина одной стороны треугольника не может превосходить сумму длин двух других его сторон.
Например, множество действительных чисел с расстоянием d(x, у) = |х – у| является метрическим пространством.
Объединим геометрические свойства, характерные для метрических пространств, и алгебраические свойства линейных пространств. Это можно сделать, если определить действительное число, характеризующее «размер» элемента в ЛП. Такое число называется нормой элемента и обозначается ||х||.
Норма должна удовлетворять следующим аксиомам:
- ||х|| >= 0;
- ||?х|| = |?| ||х||;
- ||х + y|| <= ||х|| + ||y||.
С учетом аксиомы о наличии у каждого элемента противоположного ему элемента в качестве метрики можно выбрать величину d(x, y) = ||х – y||. Тогда ЛП становится нормированным линейным пространством. Заметим, что если x — это вектор, то норма — это его длина, или расстояние от конца вектора до начала координат.
Последним шагом в развитии структуры пространства является введение дополнительной геометрической характеристики — скалярного произведения двух элементов (х, у). Определим это произведение для комплексного линейного пространства. Тогда скалярное произведение для действительного пространства будет его частным случаем.
Скалярное произведение должно удовлетворять следующим условиям:
1) (x, y) = (y, x)*, где звездочкой обозначена комплексно сопряженная величина;
2) (?х, y) = ?(х, y);
3) (x1 + x2, y) = (x1, y) + (x2, y);
4) (x, x) >= 0.
Важным следствием приведенного определения скалярного произведения является то, что величина является нормой в линейном пространстве.
С другой стороны, т.е. скалярное произведение определяет норму, которая в свою очередь определяет метрику. Следовательно, при введении указанной метрики пространство со скалярным произведением становится метрическим.
Линейное метрическое пространство, в котором норма вводится с помощью скалярного произведения, называется “евклидовым пространством”, или “пространством Евклида”.
В заключение отметим одно важное свойство. Два элемента пространства х и у называются ортогональными только в том случае, если их скалярное произведение равно нулю, т.е. (x, y) = 0.
Пространства, применяемые в теории электрической связи
Пространство Евклида (Rn). Элементами данного пространства являются либо вещественные векторы, либо комплексные векторы с размерностью n. Соответственно в первом случае имеем вещественное пространство Евклида (ВПЕ), а во втором — комплексное пространство Евклида (КПЕ).
Разложение вектора по координатному базису в ВПЕ имеет вид (2.2).
Скалярное произведение векторов х и у в этом случае
норма вектора определяется соотношением
а метрика вычисляется как
В КПЕ скалярное произведение двух комплексных векторов (Формула) запишем в виде
где * — обозначение комплексного сопряжения.
Норма в этом случае имеет вид
а метрика определяется выражением
Например, если дано КПЕ с размерностью
где (Формула) — произвольные точки пространства, норму и метрику элемента в данном пространстве соответственно можно определить следующим образом:
Пространство Гильберта. При стремлении n к бесконечности ВПЕ и КПЕ преобразуются соответственно в бесконечномерные вещественное пространство Гильберта (ВПГ) и комплексное пространство Гильберта (КПГ). Элементами этих пространств являются вещественные x(t) или комплексные (Формула) функции времени, которые могут быть заданы либо в конечном интервале времени (например, (Формула) или t ? [0, T]), либо в бесконечном интервале времени: t ? (–?, ?). Пространства Гильберта при этом соответственно обозначаются (Формула) или (Формула).
Рассмотрим случай ограниченного интервала времени Т. Тогда для ВПГ (Формула) скалярное произведение определяется в виде
норма
а метрика (расстояние между точками ВПГ задается соотношением
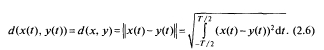Пусть x(t) — напряжение на резисторе с сопротивлением 1 Ом. Тогда (Формула) — мгновенная мощность, а квадрат нормы — это энергия, выделяемая на резисторе за время Т.
Заметим, что если в ВПГ сигналы x(t) и y(t) ортогональны, то их скалярное произведение равно нулю:
Для КПГ характеристики пространства вводятся следующим образом.
Скалярное произведение
Если в качестве (Формула) и (Формула) рассматриваются комплексные сигналы, то при равенстве скалярного произведения этих сигналов нулю их считают ортогональными в усиленном смысле. Впервые это понятие ввел Л.М. Финк.
В каналах связи со случайной фазой применение сигналов, ортогональных в усиленном смысле, обеспечивает наибольшую помехоустойчивость (см. гл. 8). Это объясняется следующим свойством этих сигналов: при сдвиге фаз составляющих какого-либо сигнала на произвольный угол их ортогональность сохраняется.
Норма в КПГ определяется следующим образом:
а метрика задается выражением
Рассмотрим теперь характеристики пространства (Формула) в случае, когда t ? (–?, ?). Возьмем КПГ, в котором элементы пространства — это комплексные функции, заданные в бесконечном интервале времени. Очевидно, что соотношение характеристик ВПГ определяется соотношением характеристик КПГ, если перейти от комплексных функций к вещественным. Здесь возможны два варианта:
1) 
— это функции, интегрируемые с квадратом (норма и энергия ограничены);
2)
— это функции, неинтегрируемые с квадратом (норма и энергия неограничены).
Второй вариант возможен, например, для периодического сигнала, у которого энергия бесконечна.
В первом варианте скалярное произведение, норма и метрика определяются выражениями (2.4), (2.5), (2.6), если в интегралах, входящих в эти выражения, конечные пределы заменить на бесконечные (–?, ?).
Во втором варианте скалярное произведение определяется следующим образом:
а норма и метрика вводятся через скалярное произведение:
Разложение произвольного сигнала x(t) по базису пространства (Формула) или (Формула) имеет вид (2.3).
Пример 2.1. Вычислим норму радиоимпульса с прямоугольной формой огибающей (рис 2.7).
Импульс существует на отрезке времени t ? (0, T) и описывается функцией (Формула).
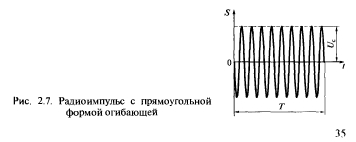
Рис. 2.7. Радиоимпульс с прямоугольной формой огибающей
В соответствии с выражением (2.5), учитывая пределы интегрирования (0, Т), запишем
.
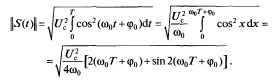Если длительность импульса намного больше периода высокочастотного колебания, т.е. (Формула), то независимо от значений (Формула) и (Формула)
Пример 2.2. Рассмотрим геометрическую интерпретацию характеристик пространства (Формула) для четырехпозиционного сигнала с фазовой модуляцией (ФМ4), который можно задать соотношением
Норма этого сигнала
где ? — энергия сигнала, постоянная для всех значений j.
Представим сигнал Sj(t) в виде
Введем базисные функции:
Эти функции являются ортонормированными (т. е. их скалярное произведение равно нулю, а норма равна единице) и линейно независимыми. Им соответствуют взаимно-перпендикулярные оси, которые обозначим (Формула) и (Формула). Разложение по координатному базису для сигнала Sj(t) имеет вид
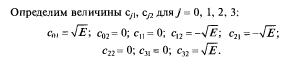
Совокупность из двух чисел для j = 0, 1, 2, 3 задает вектор в двухмерном пространстве (см. рис. 5.4, а).
Точки, соответствующие концам векторов, отмеченные на рис. 5.4, а называются сигнальными, а полученная фигура — соответственно сигнальным созвездием для сигнала ФМ4.
Расстояние между сигналами Sk(t) и Si(t) определяется непосредственно как расстояние между сигнальными точками: dm = = du = 2yiE~; dm = dn = d22 = d}0 = yf2E.
Здесь и далее встречается запись амплитуды сигнала в виде (Формула), тогда как в литературе обычно гармоническое колебание определяется выражением
где Uc — максимальное значение амплитуды, которое в (Формула) раз больше ее эффективного значения, т.е. Uc = v2Ucp.
Если сигнал считать током или напряжением на нагрузке с сопротивлением 1 Ом, то его средняя мощность (Формула). Тогда (Формула). Так как Р = ? / ? (где ? — средняя энергия, ? — длительность элемента сигнала) окончательно запишем
