onetwoclick.ruОбобщенный ряд Фурье
Пусть в комплексном пространстве Гильберта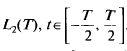 
задана полная система комплексных ортогональных функций {?,(0}, где i = 1, 2, … ?.
Система ортогональных функций называется полной, или замкнутой, если не существует непрерывной функции, не равной нулю тождественно и ортогональной ко всем функциям системы.
Функции являются попарно ортогональными, т.е. можно записать:
Если норма функций ||?i(t)|| = 1, то функции называются ортонормированными. Можно также показать, что функции являются линейно-независимыми и, следовательно, образуют координатный базис, при котором справедливо разложение (2.3). В этом случае говорят, что задан ортогональный (или ортонормированный) базис.
Пусть некоторый сигнал S(t) является сигналом с интегрируемым квадратом, который можно представить в виде ряда
— коэффициенты разложения в ортогональном базисе.
Определим коэффициенты разложения ci, для чего умножим обе части равенства на базисную функцию с произвольным номером j и произведем интегрирование по времени:
Поскольку базис является ортогональным, то в правой части равенства останется только один член суммы с номером i = j. Тогда
Иными словами, коэффициент разложения равен скалярному произведению сигнала S(t) и базисной функции.
Выражение (2.8), в котором коэффициенты определяются равенством (2.9) при i = j, называется обобщенным рядом Фурье и ему можно дать геометрическую трактовку. Коэффициенты обобщенного ряда Фурье являются проекциями вектора сигнала на базисное направление, т. е. на ортогональные оси (единичные орты).
В качестве ортогонального базиса в ТЭС широко применяется система тригонометрических (гармонических) функций.
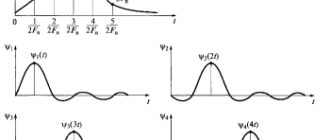
(Подробнее это будет рассмотрено далее.) Кроме того, в качестве примера можно рассмотреть использование ортогональных функций Уолша, представляющих собой систему функций типа прямоугольных волн, первые четыре из которых показаны на рис 2.8. В общем случае функции Уолша могут быть построены на основе известных в математике матриц Адамара. Эти функции удобно задавать на отрезке t ? [0, T], где они равны ±1, их принято обозначать wal(k, ? ), где k — номер функции Уолша; ? = t / T — безразмерное время.
Рис. 2.8. ВременнЫе диаграммы первых четырех функций Уолша
Представление сигнала в виде обобщенного ряда Фурье на основе функций Уолша имеет вид
Для проверки свойства ортогональности найдем скалярное произведение, например, первой и второй функций Уолша:
Помимо ортогональности функции Уолша обладают еще свойством “мультипликативности”, т.е. произведение любых двух функций Уолша также является функцией Уолша:
wal(i, ?)wal(k, ?) = wal(p, ? ),
где p = i ? k; ? — знак сложения по модулю 2.
Для такого сложения числа i и k представляются в двоичной форме и суммируются следующим образом:
0 ? 0 = 0; 1 ? 1 = 0; 1 ? 0 = 1; 0 ? 1 = 1.
Например: i = 1 => 001 (двоичн.), k = 3 => 011 (двоичн.), тогда 001 ? 011 = 010 => 2 (десятичн.).
Иными словами, wal(1, ?)wal(3, ?) = wal(2, ?), в чем нетрудно убедиться.
К функциям Уолша можно применять логические операции, поэтому они находят широкое применение в устройствах формирования и цифровой обработки сигналов на базе микропроцессоров. Сигналы на основе функций Уолша используются в цифровых многоканальных системах передачи информации. В настоящее время они также применяются в сотовой связи на основе стандарта CDMA и его модификаций.
