Понятие функции корреляции: свойства автокорреляционной функции, формула Рэлея—Парсеваля

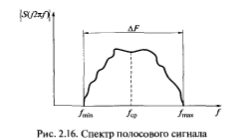
Для непериодических сигналов S1(t) и S2(t) функция взаимной корреляции определяется следующим выражением:
где ? > 0 — некий временной отрезок.

С учетом приведенных ранее свойств преобразования Фурье запишем:

где S*(j?) — величина, комплексно-сопряженная с S(j?).

Можно записать также следующее выражение:
из которого при ? = 0 несложно получить
Последнее выражение представляет собой “обобщенную формулу Рэлея—Парсеваля”, которая показывает, что скалярное произведение двух комплексных сигналов выражается через их спектральные плотности.

Введенная функция взаимной корреляции позволяет с единых позиций описывать различие сигналов по форме, а также их взаимное расположение на оси времени. Поясним это на примере.

Пусть сигналы S1(t) и S2(t) ортогональны, т.е.

При прохождении этих сигналов через различные устройства в некоторых случаях оказывается, что сигнал S2(t) будет сдвинут на время ? относительно сигнала S1(t), и наоборот. Поэтому взаимокорреляционную функцию можно считать мерой «устойчивости» ортогонального состояния при сдвигах сигналов во времени.

Помимо данной характеристики для количественной оценки степени отличия сигнала S(t) и его же смещенной во времени копии S(t + ?) вводят автокорреляционную функцию, равную скалярному произведению сигнала и его копии.

В приведенном ранее выражении заменим S1(t) = S2(t) = S(t), тогда

При ? = 0 получим равенство Парсеваля для непериодических сигналов:
Поясним физический смысл этого равенства: если считать S(t) напряжением или током на нагрузке 1 Ом, то полная энергия сигнала, развиваемая на этой нагрузке, будет равна энергии всех его частотных составляющих.

Отметим кратко свойства автокорреляционной функции.

1. Ее четность, т. е. Bs(?) = –Bs(?). Заметим также, что функция взаимной корреляции не является четной относительно аргумента ?
2. При любом значении временного сдвига ? модуль автокорреляционной функции не превосходит энергии сигнала: | ?s{?)| <= ?s(0) = Es.
3. Автокорреляционная функция имеет вид симметричной кривой с центральным максимумом, который всегда положительный. В зависимости от вида сигнала S(t) эта кривая может быть монотонно убывающей или колеблющейся.