Аналитические сигналы: огибающая, мгновенная фаза и мгновенная частота сигнала

Общие сведения

Пусть имеется гармоническое колебание

где Sm, ?0, ? — соответственно амплитуда, частота и начальная фаза сигнала; ?(t) — текущая фаза сигнала.

Этот же сигнал можно представить в виде

где — сопряженный сигнал, полученный из исходного сигнала поворотом его фазы на –?/2.

На комплексной плоскости такой сигнал S изображается в виде вектора, как показано на рис. 2.14.

Негармонические сигналы подобно сигналу (2.24) можно представить в виде процесса с изменяющейся амплитудой (огибающей) Sm(t) и полной фазой ?(t), т.е. S(t) = Sm(t) cos?(t). Однако такое представление в общем случае является неоднозначным.

Действительно, пусть задан сигнал S(t). Выбрав для него произвольную функцию S1(t) и считая (Формула), а (Формула), получим (Формула).

Выбрав затем другую функцию S2(t), можно получить другой набор «амплитуд» и фаз: (Формула) и т.д..

Рис. 2.14. Геометрическое представление комплексного сигнала

Для того чтобы представление было однозначным, как в случае гармонического сигнала, сопряженный сигнал должен быть получен из исходного сигнала посредством поворота всех его гармонических составляющих на –?/2.

Рассмотрим теперь сигнал без постоянной составляющей, представленный в виде ряда
Определим для него сопряженный сигнал из исходного сигнала посредством поворота всех его составляющих на –?/2:

Тогда комплексный сигнал будет иметь вид
(25)

а его реальная часть
Отметим, что сопряженный сигнал (Формула) можно получить из исходного, не прибегая к спектральным представлениям, а используя интегральное преобразование Гильберта:

(26)

Исходный сигнал S(t) получим из сопряженного сигнала с помощью обратного преобразования Гильберта:
Функция, называемая ядром преобразования Гильберта, имеет разрыв при t = ?, поэтому интегралы следует понимать в смысле их главного значения, например:

Часто применяется символическая запись преобразований Гильберта:

Нетрудно увидеть, что прямое преобразование Гильберта эквивалентно прохождению сигнала S(t) через фильтр с импульсной характеристикой (Формула), а обратное преобразование Гильберта эквивалентно прохождению сопряженного сигнала (Формула) через фильтр, импульсная характеристика которого (Формула).

Действительно, можно записать
(Формула).

Подставив в это выражение импульсную характеристику вида (Формула), получим формулу (2.26).

Дадим теперь определение рассмотренного сигнала.

Комплексный сигнал, полученный на основе преобразования Гильберта, называется “аналитическим” и записывается в виде выражения (2.25), где исходный сигнал есть реальная часть аналитического сигнала. Заметим, что выражение (2.25), в котором S(t) и (Формула) связаны между собой преобразованиями Гильберта, во-первых, позволяет получить однозначное представление вида (2.24), а во-вторых, обусловливает ряд важных свойств сигнала (Формула), из-за которых он получил название «аналитический».

Приведем (без доказательства) лишь важнейшие свойства аналитического сигнала, используемые в теории связи.

1. Преобразования Гильберта являются линейными. Так, для прямого преобразования Гильберта это свойство можно записать в виде
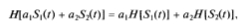
   причем при любых постоянных a1 и a2. Справедливость этого свойства следует непосредственно из выражений (2.26) и (2.27).
2. Преобразования Гильберта от постоянной величины тождественно равны нулю, т.е. 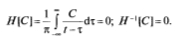Это свойство следует из того факта, что ядро преобразования Гильберта есть нечетная функция аргумента ? относительно точки t = ?, следовательно, интеграл от нечетной функции (Формула) в пределах (–?, ?) равен нулю.
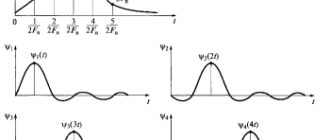
3. Если при каком-нибудь t = ? исходный сигнал достигает экстремума (максимума или минимума), то в окрестности этой точки сопряженный сигнал проходит через нуль. Сказанное иллюстрирует рис. 2.15, где совмещены графики S(?) (рис. 2.15, а) и ядра преобразования (Формула) (рис. 2.15, б) в точке t, где функция имеет максимум. Результат преобразования Гильберта (Формула) показан на рис. 2.15, в.

Нетрудно увидеть, что функция (Формула) является нечетной функцией аргумента ?, а значит, интеграл от нее в симметричных пределах (–?, ?) будет равен нулю.

4. Преобразование Гильберта от гармонических сигналов имеет вид
где.

Очевидно, что для положительных частот
H[cos?t] = sin?t;
H[sin?t] = –cos?t.

Доказательство каждого из указанных свойств следует из анализа сведений, приведенных в данном подразделе.

5. Сдвиг фаз всех составляющих действительного сигнала на угол ? соответствует умножению аналитического сигнала на (Формула), т.е. аналитический сигнал после поворота фаз, откуда легко вычислить и действительный сигнал:

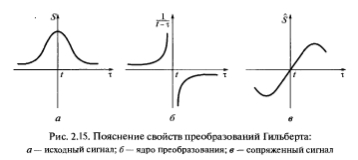
Рис. 2.15. Пояснение свойств преобразований Гильберта:
а — исходный сигнал; б — ядро преобразования; в — сопряженный сигнал

Использование понятия аналитического сигнала для определения формы действительного сигнала после поворота фаз всех его спектральных составляющих на один и тот же угол ? существенно облегчает задачу нахождения действительного сигнала. В противном случае для этого было бы необходимо с помощью преобразования Фурье найти комплексную спектральную плотность, произвести смещение фаз и затем проделать обратное преобразование Фурье.

6. Сдвиг частот всех составляющих сигнала на некоторую величину f0 при f > 0 или f < 0 (преобразование частоты сигнала, причем само изменение частоты f0 может быть как положительным, так и отрицательным) соответствует умножению аналитического сигнала (Формула) на множитель (Формула), т.е.
откуда легко найти и действительный сигнал:

Без использования понятия аналитического сигнала решить эту задачу также было бы весьма сложно.

7. В спектре аналитического сигнала содержатся только положительные частоты. Спектр, полученный посредством преобразования Фурье, имеет вид

Аналогично в спектре комплексно-сопряженного аналитического сигнала

содержатся только отрицательные частоты:

Данные соотношения вытекают из формулы Эйлера.

8. Произведение аналитического сигнала (Формула) и сопряженного с ним аналитического сигнала (Формула) равно квадрату огибающей исходного действительного сигнала S(t):
Таким образом, модуль аналитического сигнала (Формула) равен огибающей сигнала, т.е. (Формула).

Огибающая, мгновенная фаза и мгновенная частота сигнала

Комплексный сигнал, как известно, можно представить в экспоненциальной форме:
откуда следует, что

Решая два последних уравнения относительно Sm(t) и ?(t), найдем

Величина Sm(t) в этих выражениях называется мгновенной амплитудой, или огибающей, сигнала, а величина ?(t) — мгновенной фазой сигнала. Производная от мгновенной фазы во времени (если она существует), называется мгновенной круговой частотой сигнала:

Из формулы (2.31) следует, что Sm(t) >= S(t), причем равенство имеет место при тех значениях t, для которых S(t) > 0. Легко убедиться, что в этих точках производная огибающей совпадает с производной сигнала, т.е. Sm(t) = S(t) (откуда и название — огибающая сигнала).

 Узкополосные сигналы

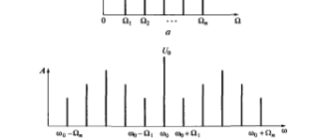
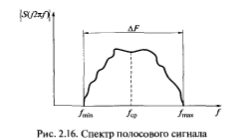
В радиотехнике и ТЭС широко применяются так называемые узкополосные сигналы, которые являются полосовыми со спектром, показанным на рис. 2.16, но ширина их спектра значительно меньше средней частоты, т.е. (Формула), где (Формула), а (Формула)— соответственно средняя, максимальная и минимальная частоты спектра сигнала.

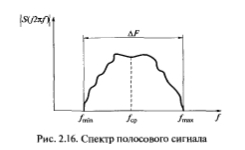
Рис. 2.16. Спектр полосового сигнала

Для узкополосных сигналов (и помех) представления (2.28) и (2.29) особенно удобны, так как в этом случае огибающая и мгновенная частота оказываются медленно изменяющимися функциями по сравнению с cos?(t) и, следовательно, по сравнению с самим сигналом S(t). При этом формулу (2.29) удобно записать следующим образом:
 причем

Возможно и преобразование соотношения (2.28) вида

Здесь
 представляет собой функцию времени, называемую комплексной огибающей сигнала S(t). Модуль этой функции является обычной огибающей, а аргумент — мгновенной начальной фазой ?(t).

Комплексную огибающую можно также представить в виде

Здесь действительные функции времени (Формула) и (Формула) являются квадратурными составляющими комплексной огибающей или низкочастотными квадратурными составляющими. С их помощью сигнал можно представить в виде суммы:
 что следует из выражений (2.34) и (2.37).

Учитывая «медленность» изменения функций (Формула) и (Формула) по сравнению с (Формула) и (Формула) из выражений (2.38) можно получить сопряженный сигнал:

Подставив выражения (2.38) и (2.39) в формулу (2.31), нетрудно убедиться, что Sm(t) — огибающая сигнала.

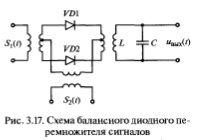
Схема, изображенная на рис. 2.17, иллюстрирует процесс формирования низкочастотных квадратурных составляющих сигнала.

Обратим особое внимание на следующее: нельзя путать понятия спектральных составляющих и мгновенной частоты, так как в первом случае частоты, входящие в спектр, не зависят от времени, а во втором — мгновенная частота есть функция времени, которая определяет скорость изменения фазы. Спектр сигнала можно измерить с помощью прибора — спектроанализатора, который выполняет приближенное преобразование Фурье. Мгновенная частота измеряется частотным детектором, работа которого будет рассмотрена далее, но по существу он реализует выражение (2.33).

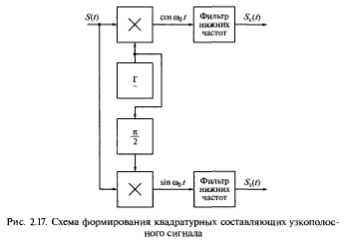
Рис. 2.17. Схема формирования квадратурных составляющих узкополосного сигнала