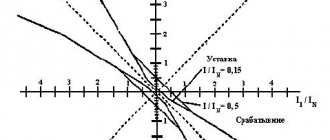
onetwoclick.ruКлассификация сигналов
В теории электрической связи при описании сигналов и помех возникает задача поиска математических моделей, которые с необходимой степенью точности отображали бы реальные процессы в каналах передачи информации. Поскольку сигналы являются электрическими колебаниями, изменяющимися во времени, то их базовой математической моделью должна быть временнАя функция, т.е. функция, значения которой изменяются во времени.
Различают сигналы детерминированные и случайные.
“Детерминированным” называется сигнал, мгновенные значения которого в любой момент времени можно предсказать с вероятностью, равной единице.
Например, при ? -> 0 сигнал ?(t, ?) переходит в единичную функцию включения (рис. 2.1):
Функция включения описывает процесс перехода некоторого физического объекта из нулевого состояния в единичное. Переход осуществляется по линейному закону за время t = 2?. При ? -> 0 в пределе переход производится мгновенно. Данная математическая модель получила название функции Хевисайда.
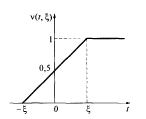
Рис. 2.1. Функция Хевисайда (функция включения)
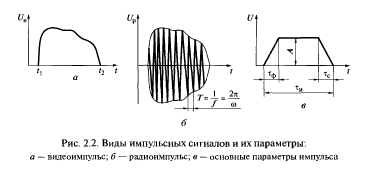
Рис. 2.2. Виды импульсных сигналов и их параметры:
а — видеоимпульс; б — радиоимпульс; в — основные параметры импульса
Важный класс сигналов представляют собой “импульсные” сигналы, под которыми понимают колебания, существующие только на конечном отрезке (в интервале) времени. При этом различают видеоимпульсы и радиоимпульсы (рис. 2.2).
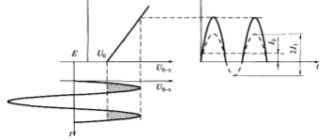
Видеоимпульсу Uв(t) >= 0 соответствует радиоимпульс Uр(t) = Uв(t) cos(?t + ?), где Uв(t) — огибающая радиоимпульса; cos(?t + ?) — высокочастотное заполнение; ?, ? — соответственно частота и фаза сигнала, имеющие произвольные значения. В ТЭС видеоимпульсы принято задавать амплитудой (А), длительностью импульса (?и), длительностью фронта (?ф) и длительностью спада (?с). Происхождение термина “видеоимпульс” объясняется тем, что данные колебания впервые стали применяться в технике телевидения.
Например, импульсный сигнал прямоугольной формы в пределе при ? -> 0 переходит в ?-функцию (рис. 2.3, 2.4):
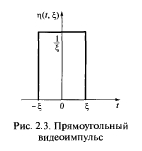Рис. 2.3. Прямоугольный видеоимпульс
Рис. 2.4. Определение ?-функции
Дельта-функция (функция Дирака) везде равна нулю за исключением точки t = 0, в которой
Дельта-функция обладает важным свойством, называемым “фильтрующим”:
Физический смысл фильтрующего свойства заключается в том, что интеграл по времени от произведения непрерывной функции и дельта-функции равен значению этой непрерывной функции в точке, где сосредоточен ?-импульс.
Соответствующая схема измерения мгновенных значений аналогового сигнала в точке t0 показана на рис. 2.5. Точность измерения S (t0) зависит от ширины прямоугольного видеоимпульса, который приближенно представляет собой ?-функцию, широко применяемую в теории электрической связи.
Детерминированные сигналы можно подразделить на периодические и непериодические. Рассмотренные ранее сигналы являются непериодическими.
“Периодическим” называется повторяющийся во времени сигнал, для которого справедливо условие
S(t) = S(t ± kT), где k — любое целое число; Т — период, являющийся конечным отрезком.
Например, периодическим является гармонический сигнал S(t) =U cos(?t + ?), –? < t < ?. Здесь U, ? = 2? / ?; ? — соответственно постоянные амплитуда, угловая частота и начальная фаза. Такой сигнал широко применяется в качестве переносчика информации при формировании модулированных сигналов.
“Случайными” называются сигналы, значения которых заранее неизвестны и могут быть предсказаны только с некоторой вероятностью, меньшей единицы. Например, электрические колебания, соответствующие речевому сигналу, музыке или последовательности знаков телеграфного кода при передаче неповторяющегося текста.
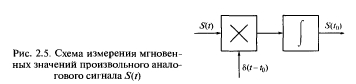
Рис. 2.5. Схема измерения мгновенных значений произвольного аналогового сигнала S(t)
Отметим, что любой сигнал, несущий в себе информацию, должен быть обязательно случайным. Приведенные ранее детерминированные сигналы, являющиеся полностью известными, информации не переносят.
Сигналы также подразделяются на одномерные и многомерные. “Одномерным” называется сигнал, который описывается одной функцией времени. Примером такого сигнала является напряжение на зажимах цепи или ток в ветви.
“Многомерным” (“векторным”) называется сигнал, образованный некоторым упорядоченным множеством одномерных сигналов (Формула), где ? — размерность сигнала. Примером такого сигнала может служить последовательность посылок на выходе кодера, т.е. кодовая комбинация, или система напряжений на зажимах многополюсника.
Наконец, сигналы могут быть “дискретными” и “непрерывными”, как во времени t, так и по уровню, о чем уже говорилось при рассмотрении сообщений.
