onetwoclick.ruНеобходимость дискретного преобразования Фурье
До сих пор мы рассматривали аналоговые (непрерывные) сигналы. Однако в настоящее время при формировании и обработке сигналов S(t) зачастую используются выборки, которые возникают при дискретизации непрерывного сигнала. В результате получают последовательность отсчетных значений сигнала S(t) в точках. Ясно, что для таких сигналов неприменим аппарат преобразований, основанный на интеграле Фурье. Для них существует особый математический аппарат, называемый дискретным преобразованием Фурье (ДПФ).
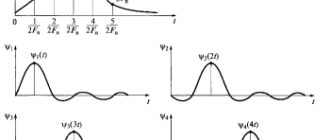
Рассмотрим N-мерное комплексное евклидово пространство, в котором можно ввести следующую систему базисных функций, называемых “базисом Фурье” (элементами базиса являются векторы):
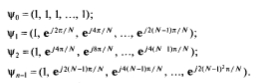
Число cxp(j2nnk/N) является k-й составляющей n-го базисного вектора. При любых n и k данное число представляет собой значение корня N-й степени из единицы в поле комплексных чисел.
Скалярное произведение базисных функций
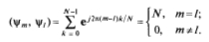
Здесь сумма обращается в нуль при m != l, поскольку все слагаемые являются комплексными числами с единичным модулем и линейно нарастающим аргументом.
Базис Фурье ортогонален, но не нормирован к единице.
Найдем коэффициенты разложения некоторого сигнала S по базисным функциям:
Для этого умножим обе части данного равенства скалярпо на базисный вектор ? с номером n:
Поскольку базисные функции являются ортогональными, в правой части этого уравнения отлично от нуля одно слагаемое с номером k = n. Поэтому
Тогда
Выражение (2.22) определяет последовательность коэффициентов, образующих дискретное преобразование Фурье.
Если известны коэффициенты разложения, т.е. комплексные амплитуды (Формула), при (Формула), можно найти отсчетные значения сигнала Sk, выполнив обратное дискретное преобразование Фурье (ОДПФ):
Выражения (2.22) и (2.23) являются по существу дискретными аналогами обычной пары преобразований Фурье для непрерывных сигналов.
Свойства дискретное преобразование Фурье
Отметим некоторые свойства ДПФ.
- Дискретное преобразование Фурье является линейным преобразованием, т.е. сумме (разности) сигналов соответствует сумма (разность) их ДПФ.
- Число коэффициентов разложения (Формула), где (Формула), в ДПФ равно числу отсчетов сигнала, т. е. N. При n = ? коэффициент (Формула).
- Коэффициент (Формула) (постоянная составляющая) представляет собой среднее значение всех отсчетов сигнала:
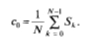
- При четном N из формулы (2.22) получим
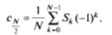
- Если отсчетные значения сигнала Sk — вещественные числа, то коэффициенты разложения ДПФ, номера которых расположены симметрично относительно N / 2, образуют комплексно-сопряженные пары:
Коэффициенты (CN/2+1 ···> CN-1) соответствуют отрицательным частотам. Поэтому при изучении амплитудного спектра они не дают дополнительной информации.
В заключение отметим следующее. При вычислении N коэффициентов ДПФ необходимо выполнить (N2) операций умножения. Если обрабатываются большие массивы, т. е. когда N >= 1000, применять ДПФ и ОДПФ в реальном масштабе становится затруднительным из-за ограниченного быстродействия ЭВМ. В последнее время разработаны алгоритмы быстрых преобразований Фурье (БПФ), при которых число операций умножения сокращается примерно до NlogN. Такие операции в курсе ТЭС не изучаются, они являются предметом рассмотрения в специальных курсах и при детальном изучении вопросов цифровой обработки сигналов.
