 Рассмотрим основные этапы построения такого автомата.
Рассмотрим основные этапы построения такого автомата.
Построение граф–схемы алгоритма операции умножения.
Граф–схема алгоритма представляет собой связанный граф со следующими основными типами вершин: начальная, конечная, операторная и условная.
При составлении графа руководствуются следующими правилами:
? граф–схема алгоритма должна содержать одну начальную, одну конечную и конечное число операторных и условных вершин;
? входы и выходы различных вершин соединяются дугами, направленными от выхода к входу. При этом выход каждой вершины соединяется только с одним входом;
? в каждой операторной вершине записывается микрокоманда
Y
к
, представляющая собой совокупность управляющих сигналов {у
n
}, или микроопераций, выполняемых на одном временном интервале (такте);
? в каждой условной вершине записывается одно из логических условий Х
i
;
? между любой вершиной и конечной вершиной должен существовать, по крайней мере, один путь.
Для наглядности построения граф–схемы и понимания сути алгоритма операции умножения в табл. 1.3.1 приведены используемые для операции умножения микрокоманды
Y
к
и логические условия X
i
. 
Для операции умножения можно построить несколько граф–схем алгоритма, каждая из которых определяет свою структуру управляющего автомата и последовательность его функционирования.
На рис. 1.3.1 приведен вариант граф–схемы алгоритма операции умножения двоичных чисел с проверкой содержимого счетчика СТ на выходе цикла. Ее особенностью является наличие двух условных вершин X1 = ? для проверки выходного сигнала триггера, выполняемой для двух значений младшего разряда регистра
RG2(X2 = 0
и
X2
=
1).
Построение графа переходов управляющего автомата.
Управляющий автомат можно строить как аппарат Мили или как аппарат Мура, которые описываются функцией перехода и функцией выходов:
A(t
+ 1) =
F(A(t), X(t)); Y(t) = f (A(t),
Х(
t
))
— для аппарата Мили,
A(
t
+ 1)
= F(A(t),
X(t)); Y(t) = f (A(t)
— для аппарата Мура,
где А =
{a0,….,aK–1}
— множество (К) состояний автомата; X = {
x
1
,…,
xM
}
— множество (М) входных сигналов;
Y
=
{y1,…,yN}
— множество
(N)
выходных сигналов;
t
— дискретное время
(t
= 0,1,2,3,…); А(0) = а0 — начальное состояние автомата.
Функция переходов для обоих аппаратов представляет собой состояние автомата
A(t
+ 1) в момент времени
t
+ 1 в зависимости от состояния
A(t)
и сигнала
X(t)
в момент
t.
Функция выходов для аппарата Мили определяет зависимость выходного сигнала
Y(t)
от состояния автомата
A(t)
и входного сигнала
X(t),
а для аппарата Мура — только от состояния автомата
A(t).
Построим граф переходов для автомата Мили. Граф строится в два этапа.
На первом этапе производится разметка граф–схемы алгоритма. Цель разметки — определить возможные состояния операционного (управляющего) автомата А =
{ao,….,a
К–1
}.
Правила разметки:
? символом а0 отмечается вход первой вершины, следующей за начальной, а также вход конечной вершины;
? входы вершин, следующих за операторными вершинами, отмечаются символами а1, а2, …;
? входы двух различных вершин, за исключением коренной, не могут быть отмечены одинаковыми символами;
? вход вершины может отмечаться только одним символом. Отметки состояний нанесены на граф–схеме (рис. 1.3.1) в виде крестиков. На втором этапе строится непосредственно граф переходов, вершинами которого являются состояния {ар}, а дугами — возможные изменения состояний (переходы).

Для построения графа переходов управляющего автомата вводится понятие пути от отметки а
n
к отметке а
s
(от начального состояния к конечному) на граф–схеме алгоритма (рис. 1.3.1):
anX(an, as) Y(an, as) as, (1.3.1)
где Х(а
n
,
as
)— конъюнкция (произведение) всех логических условий Хк (
k
=1,2,3,…), соответствующих условным вершинам граф–схемы на этом пути, причем Хк берут в прямой форме, если из данной вершины путь выходит по стрелке, отмеченной значением 1, и в инверсной форме, если путь выходит по стрелке, отмеченной значением 0;
Y
(а
n
, а
S
) — множество микроопераций, или микрокоманда, указанная в единственной операторной вершине, через которую проходит данный путь.
Множество путей (1.3.1) определяет множество переходов между состояниями а
n
и а
s
автомата. Допустимы пути, содержащие несколько условных вершин или не содержащие ни одной, а также пути, не содержащие операторной вершины. Рассматриваются все пути, кроме тех, в которых некоторое условие X
j
(
j
е
k
) входит как в прямой, так и в инверсной форме.
При построении графа переходов:
? каждую отметку (ар) на граф–схеме алгоритма представим в виде кружочка (с пометкой ар), отражающего вершину графа переходов;
? каждый путь (1.3.1) представим дугой, направленной из вершины а
n
в вершину а
s
. Дуга отражает переход автомата из состояния а
n
в состояние а
s
и помечается конъюнкцией Х(а
n
, а
s
) и выходными сигналами У(а
n
, а
s
), при этом:
• если в рассматриваемом пути отсутствуют логические вершины, то принимают Х(а
n
, а
s
) = 1 (т. е. осуществляется безусловный переход);
• если же отсутствует операторная вершина, то полагают
Y
(а
n
, а
s
) = у0, где
Y
0
— пустой оператор, означающий сохранение состояния, так как не выполняется никакая микрооперация.
Построенный по изложенной методике граф переходов (рис. 1.3.2) определяет закон функционирования и структуру управляющего автомата. 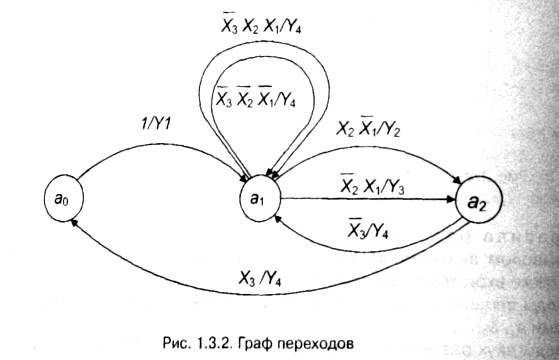
Кодирование состояний управляющего автомата.
Для фиксации состояний управляющего автомата будем использовать триггеры. Каждому состоянию управляющего автомата поставим в соответствие некоторую кодовую комбинацию, отображаемую состоянием
Q
–выходов триггеров.
Число разрядов N кода, или триггеров, можно выбрать на основании соотношения:
K
<= 2
k
, где
k
— число состояний управляющего автомата. Для рассматриваемого случая К=3, N=2. 
Выбранные коды состояний управляющего автомата приведены в табл. 1.3.2.
Структурная схема управляющего автомата представлена на рис. 1.3.3. Она содержит:
? два синхронных
RS
–триггера
Т0,
T
1
, образующих регистр хранения информации для фиксации текущего состояния операционного (управляющего) автомата с помощью выходных сигналов
Q
1
,
Q
0
;
? дешифратор
D
С
, предназначенный для преобразования двухразрядного кода
Q
1
Q
0
в сигналы состояния а0, а1, а2;
? комбинационную схему, которая вырабатывает управляющие сигналы
Y
1
,
Y
2
,
Y
3
,
Y
4
для операционного автомата и сигналы
S
0
,
R
0
,
S
1
,
R
1
для триггеров по входным сигналам X1, Х2, Х3, а0, а1, а2.
Дальнейшей задачей является построение комбинационной схемы. 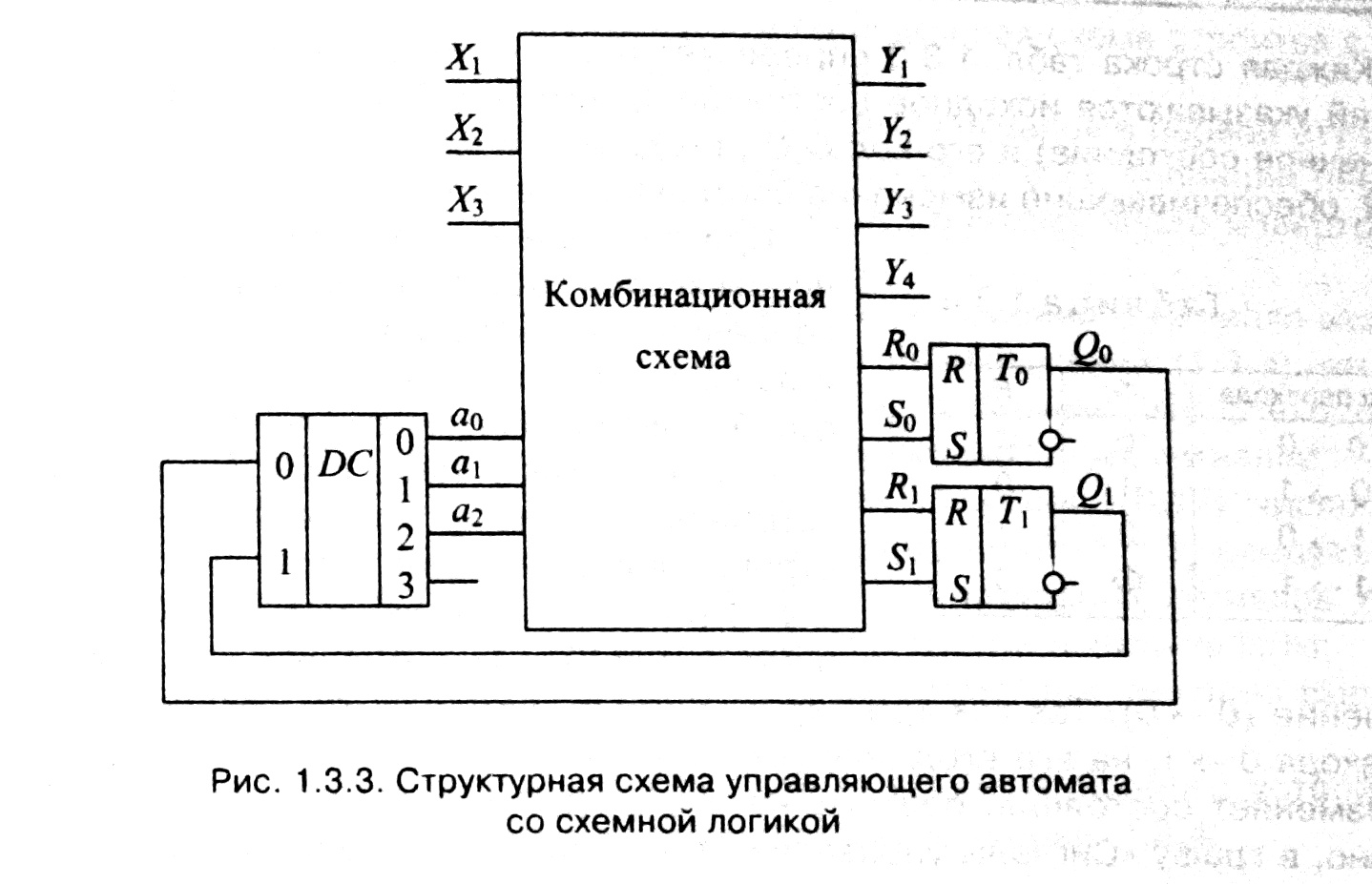
Составление таблицы функционирования комбинационной схемы.
Описание работы управляющего автомата с помощью графа переходов обеспечивает наглядность. Однако для описания комбинационной схемы с помощью структурных формул целесообразно составить таблицу, в которой для каждого перехода были бы приведены сигналы управления триггерами (табл. 1.3.3). 
Каждая строка табл. 1.3.3 определяет один переход управляющего автомата. В ней указываются исходное состояние а
n
, его код
Q
1
Q
0
, состояние перехода
as
(конечное состояние) и его код
Q
1
Q
0
, входные X и выходные
Y
сигналы и сигналы
S
,
R
, обеспечивающие изменение состояний триггеров.
При составлении таблицы функционирования используются граф переходов (рис. 1.3.2), а также сведения о кодировании состояний (табл. 1.3.2) и об изменении состояния триггеров (табл. 1.3.4, где Ф — любое значение сигнала: 0 или 1).
Покажем, как в табл. 1.3.3 заполняется графа «Сигналы управления триггерами
S
,
R
». В первой строке таблицы отражен переход из состояния
a
0
в а1. При этом младшие разряды
Q
0
кодов а0,
a
1
изменяются (0 —> 1), а старшие
Q
1
сохраняют свое значение (0 —> 0). Так как триггер Т0 должен изменить состояние и имеет вид перехода 0 —> 1, на его вход следует подать сигнал
S
0
= 1 (табл. 1.3.4). Триггер
T
1
не изменяет состояния, поэтому на его входы сигналы не подаются. Следовательно, в графу «Сигналы управления триггерами
S
,
R
» первой строки заносится только
S
0
.
Во второй и третьей строках табл. 1.3.3 состояние а1 остается неизменным, поэтому сигналы управления не подаются и в графе для
S
,
R
поставлен прочерк. В строках 4, 5, 6 изменяются младшие
Q
0
и старшие
Q
1
разряды кодов состояния а1 и а2, поэтому необходимо подавать управляющие сигналы на оба триггера. В строке 7 изменяются только старшие
Q
1
разряды кодов а1 и а0. Так как триггер
T
1
должен изменить состояние и имеет вид перехода 1 —> 0, на его вход следует подать сигнал
R
1
= 1 (табл. 1.3.3).
Запись логических выражений для комбинационной схемы.
Для каждой строки табл. 1.3.3 запишем логическое выражение в следующей форме:
? в левой части выражения перечислим величины
Y
,
S
,
R
(содержимое двух последних столбцов, представляющее собой выходные сигналы комбинационной схемы
Y
1
,
Y
2
,
Y
3
,
Y
4
,
S
0
,
R
0
,
S
1
,
R
1
);
? в правой части представим входные сигналы (Х1, Х2, Х3, а0, а1, а2) в виде конъюнкции а
n
.
X текущего (начального) состояния и условий перехода. В результате получим:
Y1, S0 = a0 . 1; Y4 = a1 . ?X3 . X2 . X1; Y4 = a1. ?X3 . ?X2 . ?X1;
Y2, R0, S1 = a1 . ?X2 . X1; Y2, R0, S1 = a1 . X2 . ?X1;
Y3, S0, R1 = a2 . ?X3; R1 = a2. X3.
( 1.3.2 )
Пользуясь (1.3.2), составим логические выражения для каждого выходного сигнала комбинационной схемы. Для этого в левой части запишем непосредственно выходной сигнал, а в правой части — дизъюнкцию (сумму) правых частей тех соотношений (1.3.2), в которые входит указанный выходной сигнал комбинационной схемы. Полученные таким образом логические выражения, или структурные формулы, для комбинационной схемы имеют следующий вид:
Y1 = a0; Y2 = a1 . ?X2 . X1; Y3 = a1 . X2 . ?X1;
Y4 = a1 . ?X3 . X2 . x1
?
a1 . ?X3 . ?X2 . ?X4
?
a2;
S0 = a0
?
a2 . ?X3 ; S1 = R0 = a1 . ?X2 . X1
?
a1 . X
2
. ?
X
1
;
R
1
=
a
2
.
(1.3.3 )
Построение
комбинационной
схемы
.
Комбинационная схема строится с помощью выражений (1.3.3) по следующим правилам:
? определяется количество инверторов для входных сигналов в первой ступени комбинационной схемы. Как следует из выражений (1.3.3), операции инвертирования выполняется над сигналами X1, Х2, Х3, поэтому число инверторов равно трем;
? определяется количество логических элементов умножения И (и число входов каждого из них) во второй ступени. Как видно из выражений (1.3.3), вторая ступень должна содержать пять элементов И. Отметим, что 3–входовые элементы И участвуют в формировании нескольких выходных сигналов;
? определяется количество логических элементов сложения ИЛИ (и число входов каждого из них) в третьей ступени. Из выражений (1.3.3) следует, что операция логического сложения выполняется для выходных сигналов
Y
4
,
S
0
и
R
0
=
S
0
, поэтому третья ступень должна содержать три элемента ИЛИ;
? производится соединение выводов логических элементов согласно выражениям (1.3.3).
Построенная по изложенным правилам схема комбинационного устройства управляющего автомата со схемной логикой приведена на рис. 1.3.4. 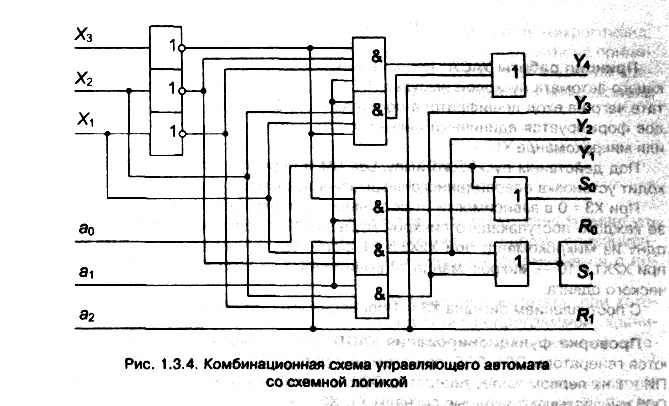
Схемная реализация УАСЛ.
Управляющий автомат служит для формирования последовательности микрокоманд из заданного набора
Y
1
,
Y
2
,
Y
З
,
Y
4
с помощью сигналов логических условий Х1, Х2, ХЗ поступающих с выходов операционного автомата. Сформированная управляющим автоматом последовательность микрокоманд поступает на входы операционного автомата и обеспечивает выполнение операции умножения двоичных чисел.
В УАСЛ входят рассмотренная выше комбинационная схема (рис. 1.3.4), дешифратор и два
RS
–триггера, предназначенных для хранения состояний операционного автомата (рис. 1.3.5). 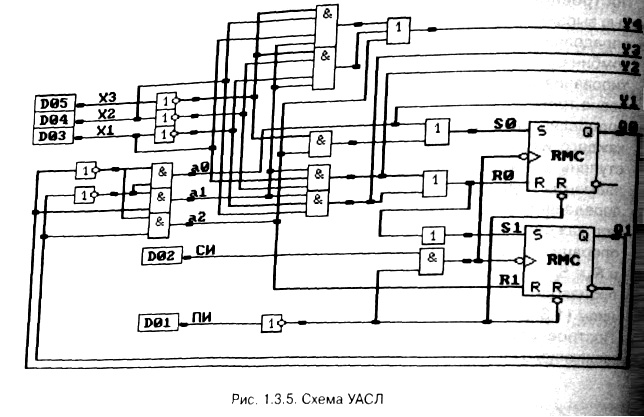
Управляющий автомат имеет три информационных входа Х1, Х2, ХЗ и два управляющих входа, на которые поступают синхроимпульсы СИ и пусковой импульс ПИ для сброса триггеров.
Принцип работы УАСЛ.
Независимо от состояния входов Х1, Х2, ХЗ управляющего автомата пусковой импульс ПИ = 1 производит сброс триггеров, в результате чего на вход дешифратора поступает код
Q
1
Q
0
= 00 и на одном из его выходов формируется единичный сигнал, соответствующий исходному состоянию
a
0
или микрокоманде
Y
1
.
Под действием пускового импульса ПИ и первого синхроимпульса СИ происходит установка операционного автомата в исходное состояние.
При ХЗ = 0 в зависимости от состояния информационных входов Х2, X1 на срезе каждого поступающего синхроимпульса СИ управляющий автомат формирует одну из микрокоманд: при Х2Х1 = 01 формируется микрокоманда
Y
2
сложения; при Х2Х1 = 10 — микрокоманда
Y
2
вычитания; при Х2Х1 = 00 или 11 — арифметического сдвига.
С поступлением сигнала ХЗ = 1 операция умножения завершается.
Проверка функционирования УАСЛ.
Для проверки работы УАСЛ используются генераторы
D
01
—
D
05
, при этом генератор
D
01
формирует пусковой импульс ПИ = 1 на первом такте, генератор
D
02
— синхроимпульсы, генераторы
D
ОЗ
,
D
04
,
D
05
вырабатывают входные сигналы Х1, Х2, ХЗ.
При выборе сигналов X1, Х2, ХЗ (табл. 1.3.5) целесообразно исходить из алгоритма умножения двоичных чисел 1011 х 0111 (см. рис. 1.2.1). 
В этом случае УАСЛ должен сформировать последовательность микрокоманд, которая использовалась при изучении работы операционного автомата на примере перемножения операндов А = 1011 и В = 0111 (рис. 1.2.4). Как видно из временных диаграмм (рис. 1.3.6), именно такая последовательность микрокоманд и получена в результате моделирования схемы УАСЛ. 

 onetwoclick.ru
onetwoclick.ru