Операционный автомат. Алгоритм умножения Бута

Операционный автомат для умножения двоичных чисел

Алгоритм умножения Бута.

При умножении по алгоритму Бута не требуется никаких дополнительных операций для определения знака произведения, т. е. старший (знаковый) разряд произведения правильно указывает его знак. Опера­ция умножения выполняется над

n

–разрядными двоичными числами, представ­ленными в дополнительном коде. Результатом операции является произведение в дополнительном коде.

Для представления положительных чисел в дополнительном коде в знаковый разряд заносится нуль, модуль двоичного числа записывается без изменения; для представления отрицательных чисел — в старший разряд записывается еди­ница, модуль двоичного числа инвертируются, после чего к младшему разряду прибавляется единица.

Таким образом, модуль преобразуется в дополнительный код только при запи­си отрицательных чисел. Поэтому при определении модуля отрицательных чисел, представленных в дополнительном коде, используется повторное преобразова­ние значащей части числа в дополнительный код.

Пример.

Число +5₁₀ в дополнительном коде получается путем записи 0 в знаковый разряд, за которым сле­дует модуль |5₁₀| = 101₂). Запись имеет вид 0101. Представление числа —5₁₀ в дополнительном коде осу­ществляется путем инверсии модуля |5₁₀| = 101₂ (010), прибавления 1 (010 + 1 =011) и записи 1 в стар­ший (четвертый) разряд — 1011. Для повышении разрядности положительных и отрицательных чи­сел в дополнительном коде в старшие разряды приписываются соответственно нули и единицы (00…0101,11…1011). Жирным Шрифтом выделены знаковые разряды.

Для определения модуля отрицательного числа 11… 1001, представленного в дополнительном коде, значащая часть числа 1… 1001 записывается в дополнительном коде: 0…0100 + 1 = 0…0101 = |5₁₀|.

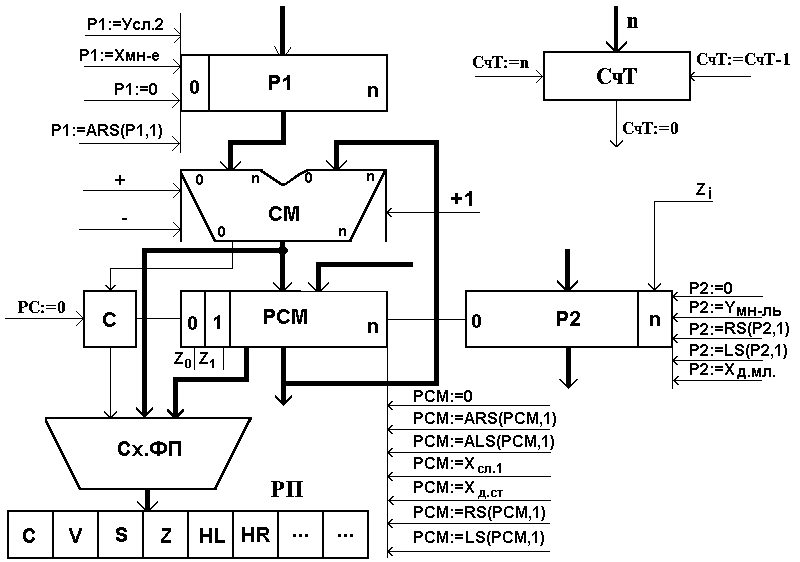
Аппаратные средства.

Для умножения двоичных чисел воспользуемся:

?

n

–разрядным регистром

RG

1

для постоянного хранения множимого А;

? двумя

n

–разрядными регистрами

RG

2

,

RG

3

, предназначенными

для

хранения промежуточных результатов и произведения. В исходном состоянии регистр

RG

2

загружается множителем

B

, в регистр

RG

3

— нулями;

? триггером Т, выходной сигнал

Q

которого используется для выявления следу­ющего действия в промессе умножения двоичных чисел;

? сумматором – вычитателем для реализации микроопераций суммирования и вычитания двоичных чисел, при этом регистры

RG

3

,

RG

2

и триггер

T

образуют (2

n

+ 1) раз рядный сдвигающий регистр. По­мимо выходного сигнала триггера (

Q

) для выявления выполняемого действия используется младший разряд регистра

RG

2

(МР

RG

2

).

В табл. 1.2.1 для различных комбинаций МР

RG

2

и

Q

приведены действия, выполняемые аппарат­ными средствами при умножении двоичных чисел по алгоритму Бута. В табл 1.2.1 обозначено:

?

R

1(

RG

3

,

RG

2

,

T

) — арифметический сдвиг содержимого составного сдвига­ющего регистра

RG

3

,

RG

2

,

T

вправо на один разряд, при котором сохраняется значение старшего разряда регистра

RG

3

;

?

RG

3

<—

RG

3

+

RG

1

,

RG

3

<—

RG

2

—

RG

1

— соответственно сложение содержимого

RG

2

с

RG

1

и вычитание из

RG

3

содержимого

RG

1

с сохранением результата в

RG

3

.

Иллюстрация умножения по алгоритму Бута.

Особенности схемной реализации операционного автомата для умножения двоичных чисел по алгорит­му Бута, а также сущность самого алгоритма рассмотрим на конкретном примере перемножения трехразрядных чисел с учетом знака:

A

х

B

= (—5)₁₀ х 7₁₀ = —35₁₀ (рис. 1.2.1). Контролируемые величины — младший разряд регистра

RG

2

и выход ной сигнал триггера

T

— выделены с помощью овала.

В исходном состоянии регистры

RG

1

и

RG

2

загружены соответственно множи­мым А = 1011 (–5)₁₀ и множителем В = 0111 (+7)₁₀ , представленными в дополни­тельном коде; в регистр

RG

2

И триггер Т занесены нули. При этом младший раз­ряд регистра

RG

2

и выходной сигнал триггера Т представляют собой комбинацию 10, следовательно, рекомендуемое действие в соответствии с табл. 1.2.1 — вы­читание со сдвигом:

RG

3

<—

RG

3

—

RG

1

;

R

1 (

RG

3

,

RG

2

,

T

) .

Операции вычитания реализуется путем сложения множимого 1011 (—5₁₀), представленного в дополнительном коде 0101 (+5₁₀) с содержимым

RG

3

, т. е. вы­полняется операция 0000 + 0101 (рис. 1.2.1).

В результате выполнения вычитания и сдвига 1 комбинация младшего разряда

RG

1

и выходного сигнала триггера Т принимает значения 11. Рекомендуемое дей­ствие — сдвиг 2, после которого комбинация младшего разряда

RG

1

и выходного сигнала триггера

T

сохраняет значения 11. Поэтому далее следует сдвиг 3, приво­дящий к комбинации 01, которая согласно табл. 1.2.1, требует сложения и сдвига 4:

RG

3

<—

RG

3

+

RG

1

;

R

1 (

RG

3

,

RG

2

,

T

).

После выполнения указанных действий получаем произведение в дополни­тельном коде. Так как знаковый разряд равен 1, путем преобразования результа­та в дополнительный код и перехода к десятичной системе счисления получаем значение произведения, равное —35.

Из рис 1.2.1 следует, что процесс умножения носит циклический характер. На каждом цикле производится проверка младшего разряда регистра

RG

2

и выход­ного сигнала триггера Т, которые будем отождествлять с логическими условиями X₂ и X₁ соответственно. Возможны три исхода проверки:

? если Х₂Х₁ = 10, то выполняется микрооперация сложения содержимого регист­ров

RG

3

и

RG

1

, и результат помещается в

RG

3

:

RG

3

<—

RG

3

+

RG

1

. Затем осуще­ствляется микрооперации арифметического сдвига вправо на один разряд содержимого составного регистра, образованного из регистров

RG

3

,

RG

2

и триг­гера

T

:

R

1 (

RG

3

,

RG

2

,

T

);

? если Х₂Х₁ = 01, то выполняется микрооперация вычитания

RG

3

<—

RG

3

—

RG

1

с последующим сдвигом

R

1 (

RG

3

,

RG

2

,

T

);

? если Х₂Х₁ = 00 или 11, то выполняется только микрооперация арифметическо­го сдвига

R

1 (

RG

3

,

RG

2

,

T

).

Число циклов

n

равно числу разрядов сомножителей (в примере

n

= 4). Поэто­му для автоматической фиксации завершения операции умножения можно ис­пользовать трехразрядный вычитающий счетчик СТ числа повторений цикла.

В исходном состоянии счетчик загружается числом

n

= 4 (100₂). По заверше­нии каждого цикла содержимое счетчика уменьшается на единицу. После 4–го цикла счетчик будет пуст (000). Если к выходам счетчика подключить логический элемент 3ИЛИ–НЁ и его выходной сигнал принять в качестве логического усло­вия Х₃, то Х₃ = 1 будет свидетельствовать о завершении 4–го цикла, или об оконча­нии операции умножения.