 Назначение АЛУ.
Назначение АЛУ.
Арифметическо–логические устройства предназначены для выполнения арифметических и логических операций над
n
–разрядными операндами А =
An
–1
…
A1A0
и
В =
Bn
–1
…
B
1
B
0
.
Вид выполняемой операции задается:
? битом М (
Mode
— режим), позволяющим выбрать арифметическую (М = 0) или логическую (
M
= 1) операцию;
? 4–разрядным кодом Е3Е2Е1Е0, позволяющим выбрать одну из 16 арифметических и 16 логических операций. Логические операции над операндами
A
и
B
выполняются поразрядно:
?
A
= ?
A
3
?
A
2
?
A
1
?
A
0
,
?
B
= ?
B
3
?
B
2
?
B
1
?
B
0
,
A
*
B
= (
A
3
*
B
3
)(А
2
* В
2
)(А1 * В1
)(А0 * В0
),
где символом « * » обозначена любая двуместная операция алгебры логики (ИЛИ, И, ИЛИ–НЕ, И–НЕ, исключающее ИЛИ и др.).
Помимо операндов на вход АЛУ подается сигнал переноса С0. Результат выполнения операции снимается с выходов в виде функций
Fi
(
i
=0,1,2,3) для отдельных разрядов.
Рассмотрим особенности АЛУ на примере 4–разрядных устройств. Основой для построения АЛУ служат СУММАТОРЫ с ускоренным переносом.
Принцип построения сумматоров.
В многоразрядных сумматорах для сложения отдельных разрядов (начиная с младшего) двоичных чисел используются полные одноразрядные сумматоры. На входы сумматора поступают сигналы
Ai
,
Bi
, 1–го разряда и сигнал С
i
переноса из предыдущего разряда, а с выхода снимаются сигналы текущего разряда
Si
суммы и переноса
Ci
+1
в следующий разряд. 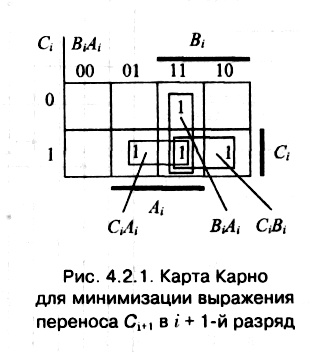
Правила функционирования полного сумматора отображены в табл. 4.2.1.
Воспользовавшись табл. 4.2.1 и картой Карно (рис. 4.2.1) составим выражения для суммы и выходного сигнала переноса:
Si
=
Ci
?
Bi
?
Ai
,
(4.2.1)
Ci
+1
=
CiBi
?
CiAi
?
BiAi
1
=
Gi
?
PiCi
,
(4.2.2)
где символами
?
и
?
обозначены операции сложения по модулю два и логического сложения.
Из (4.2.2) следует, что:
? сигнал
Gi
=
Ai
.
Bi
= 1 вырабатывается (генерируется) при наличии обоих сигналов в данном разряде (т.е. перенос происходит при А
i
= В
i
= 1), поэтому он называется функцией генерации переноса;
? сигнал Р
i
=
Ai
v
Bi
= 1 разрешает прохождение переноса С
i
= 1 на выход, поэтому он называется функцией распространения переноса. Используя (4.2.2), запишем следующие выражения для сигналов переноса:
C
1
=
G
0
?
P
0
C
0
,
C
2
=
G
1
?
P
1
C
1
=
G
1
?
P
1
G
0
?
P
1
P
0
C
0
,
C
3
=
G
2
?
P
2
C
2
=
G
2
?
P
2
G
1
?
P
2
P
1
G
0
?
P
2
P
1
P
0
C
0
;
(4.2.3)
C
4
=
G
3
?
P
3
C
3
=
G
3
?
P
3
G
2
?
P
3
P
2
G
1
?
P
3
P
2
P
1
G
0
?
P
3
P
2
P
1
P
0
C
0
=
G
?
PC
0
(4.2.4)
Выражения (4.2.3), (4.2.4) свидетельствуют о том, что для получения сигналов переноса С
i
+1
(
i
= 0, 1, 2, 3) достаточно располагать функциями
Gi
, Р
i
(по сути, входными сигналами
Ai
,
Bi
разрядов слагаемых) и сигналом внешнего переноса С0. Они описывают двухступенчатые комбинационные устройства, в первой ступени которых формируются логические произведения, а во второй — логические суммы. Поэтому можно считать, что сигналы всех переносов будут сформированы одновременно и за более короткий промежуток времени, чем в схеме многоразрядного сумматора с последовательным переносом.
Рассмотренный способ формирования переносов часто называется параллельным,
а сумматоры, построенные по этому способу, — сумматорами с параллельным переносом. 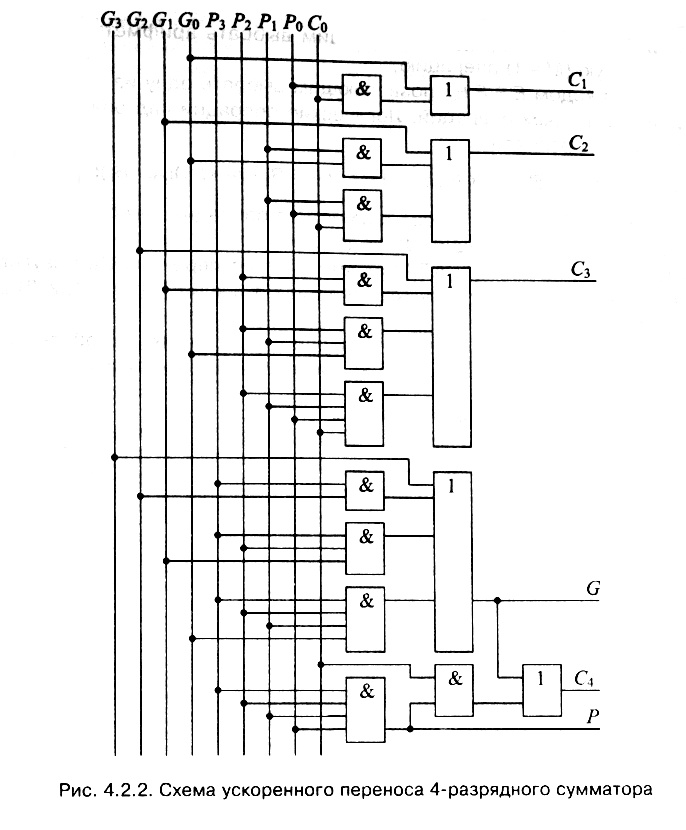
Используя соотношения (4.2.3), (4.2.4), можно построить схему ускоренного (параллельного) переноса для 4–разрядного сумматора (рис. 4.2.2). Как видно из рис. 4.2.2, схема ускоренного переноса с помощью входных сигналов С0,
Gi
,
Pi
(
i
=
0, 1, 2, 3) формирует переносы в старшие разряды С1…С4, а также функции генерации
G
и распространения
P
переносов, используемые при групповом включении 4–разрядных сумматоров.
 Отметим, что на основе 4–разрядных сумматоров можно построить сумматоры с разрядностью 8, 12, 16 и т. д. с параллельным групповым переносом.
Отметим, что на основе 4–разрядных сумматоров можно построить сумматоры с разрядностью 8, 12, 16 и т. д. с параллельным групповым переносом.
Функции АЛУ.
Для выполнения логических операций и расширения функциональных возможностей рассмотренного выше сумматора примем следующие меры:
? путем замены в (4.2.1) С
i
на С
i
?
M
создадим условия для блокировки переноса (при
M
=
1 перенос блокируется);
? вместо
разрядов А
i
и Вi
операндов
А и
В в (4.2.1) будем использовать функции
fiA
=
E
1
?
B
1
?
E
0
Bi
Ai
;
fiB
=
E
3
?
Bi
Ai
?
E
2
Bi
Ai
.
(4.2.5)
Принимая в (4.2.1)
Si
=
Fi
получаем следующее выражение для описания функций АЛУ:
Fi
= (
E
3
Bi
Ai
?
E
2
?
Bi
Ai
)
?
(
E
1
?
Bi
?
E
0
Bi
?
Ai
)
?
(
Ci
?
M
).
(4.2.6)
При М = 0 выражение (4.2.6) позволяет выявить 16 арифметических операций, а при
M
=
1 – 16 логических операций, выполняемых АЛУ. Вид выполняемой арифметической и логической операции определяется 4–разрядным кодом
E
3
E
2
E
1
E
0
. 
В табл. 4.2.2 приведены преобразования походных выражений (4.2.6) и конечные выражения (графы М = 0 и
M
=
1) для операций
Fi
АЛУ над отдельными разрядами
Ai
и
B
i
операндов. Для преобразований использовались следующие формулы:
b
?
a = b
?a
?
?b a = ? (b a
?
?b ?a); b
?
1 =
?b;
b
?
b = 0; b
?
a =
? (?b ?a); ba = ? (?b
?
?a);
Для перехода к операциям над операндами следует в полученных выражениях заменить
Ai
на
A
,
B
i
на
B
,
C
i
на С0 = 000С0, 0 на 0000, 1 на 1111, а для арифметических операций (М = 0) дополнительно — символ
?
на знак « + » арифметического сложения. 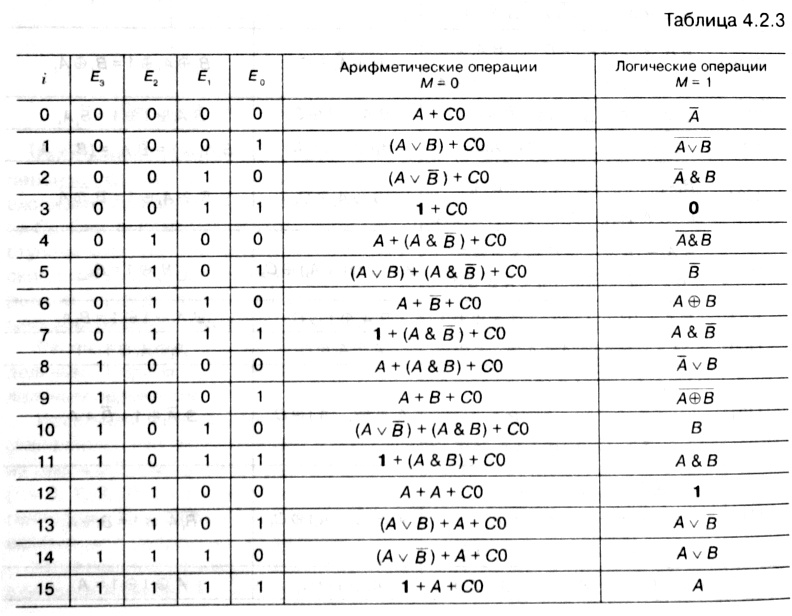
Операции, выполняемые АЛУ над входными операндами, приведены в табл. 4.2.3. При описании операций использовались следующие обозначения;
? А, В — входные 4–разрядные операнды;
? 0 = 0000, 1 = 1111 — 4–разрядные операнды со значениями каждого разряда, равными 0 и 1 соответственно;
? С0 = 000С0 — 4–разрядный операнд, самый младший разряд которого задействован для входного сигнала переноса;
? знак « + » для операции арифметического сложения операндов;
? символы
?
, &,
?
для операций логического сложения, умножения и исключающего ИЛИ операндов;
?
?
А, ?В — поразрядное инвертирование операндов
А, В.
АЛУ является универсальным устройством с точки зрения выполнения логических операций, так как выполняет все 16 возможных логических операций над двумя переменными.
Отметим некоторые особенности арифметических операций. Для расширения функциональных способностей АЛУ:
? предусмотрена возможность реализации арифметических операций со значениями входного сигнала переноса С0 = 0 и С0 = 1. При С0 = 1 на входе АЛУ появляется дополнительный операнд 0001;
? большинство арифметических операций совмещено с предварительно выполненными логическими операциями. С этой точки зрения весьма полезной является операция А +
B
+ С0 (
i
= 6), которая при С0 = 0001 позволяет получить разность операндов А – В с представлением результата в дополнительном коде. При А = 0000 и С0 = 0001 с помощью этой операции формируется дополнительный код операнда в. Для представления операнда в дополнительном коде можно использовать и другие операции, например (А
v
B
) + С0 (
i
= 2);
? имеется операция сложения двух одинаковых операндов: А + А + С0 (
i
= 12). При выполнении этой операции производится сдвиг операнда А на один разряд влево (в сторону старших разрядов) с записью в младший разряд значения сигнала входного переноса С0. Указанный сдвиг обусловлен увеличением числа А в 2 раза, что равносильно операции умножения на 2, а следовательно, для двоичных чисел сдвигу влево йа один разряд;
? имеется операция А + С0 (
i
= 0), которая при С0 = 0001 аналогична операции инкрементации (увеличения на +1), выполняемой счетчиками.
Принципы формирования переносов.
Запишем полученное выше выражение (4.2.2) для переноса в (
i
+ 1)–й разряд в виде
Ci
+1
=
Gi
?
PiCi
=
fiA
.
fiB
?
(
fiA
?
fiB
) .
Ci
,
(4.2.7)
где
fiA
,
fiB
— функции, определяемые соотношениями (4.2.2), используются в АЛУ вместо
Ai
и
Bi
.
На основании (4.2.5) и (4.2.7) запишем выражения для функций генерации и распространения переноса с учетом того, что Х.Х = Х, Х.?Х = 0, X
?
1 = 1:
Gi = fiA . fiB = (E1?Bi
?
E0Bi
?
Ai) . (E3Bi Ai
?
E2 ?Bi Ai) =
= E1E2 ?Bi Ai
?
E0E3BiAi
?
E3BiAi
?
E2 ?Bi Ai =
= (E1 + 1)E2 ?Bi Ai
?
(E0 + 1)E3BiAi = E3BiAi
?
E2 ?Bi Ai) = fiB,
(4.2.8)
p
i
= fiA
?
fi
в
= E1?Bi
?
E0Bi
?
Ai
?
E3Bi Ai
?
E2 ?Bi Ai =
= E1?Bi
?
E0Bi
?
Ai (1
?
E3Bi Ai
?
E2 ?Bi Ai) = E1?Bi
?
E0Bi
?
Ai = fiA ,
(4.2.9)
Как следует из выражений (4.2.6), (4.2.8), (4.2.9), функции
Fi
, выполняемые АЛУ, функции генерации
Gi
и распространения Р
i
переноса могут быть сформированы в одном устройстве, которое назовем формирователем.
Принципы построения АЛУ.
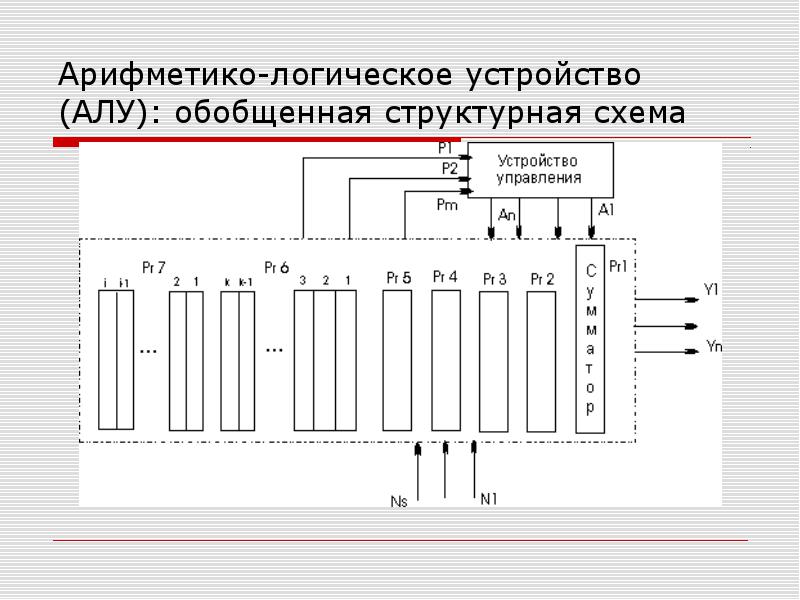
Арифметическо–логическое устройство подобно 4–разрядному сумматору можно представить как совокупность четырех идентичных формирователей Ф0–Ф3 и схемы ускоренного переноса. Работа формирователей АЛУ описывается функциями (4.2.6), (4.2.8), (4.2.9). Схема формирователя, построенная в соответствии с выражением (4.2.6), изображена на рис. 4.2.3. На входы формирователя подаются: 
? сигналы
i
–х разрядов операндов (А
i
, В
i
) и переноса
Ci
;
? сигнал М выбора вида выполняемой операции (арифметической М = 0 или логической М = 1);
? 4–разрядный код Е3Е2Е1Е0 выбора выполняемой арифметической или логической операции.
С выхода формирователя снимаются:
? результат выполненной операции для
i
–го разряда в виде функции
? сигналы для формирования переноса С
i
+1
, в следующий разряд в виде функций генерации и распространения переноса
Gi
=
E
3
Bi
Ai
?
E
2
?
Bi
Ai
,
p
i
=
E
1
?
Bi
?
E
0
Bi
?
Ai
.
При
E
3
= 1,
E
2
= 0,
E
1
= 0, Е0 = 1 (табл. 4.2.3,
i
= 9 — операция сложения двух операндов) получаем известные функции генерации и распространения переноса для прямых операндов А и
B
, при
E
3
= 0, Е2 = 1, Е1 = 1, Е0 = 0 (табл. 4.2.3,
i
= 6) — функции генерации и распространения переноса для прямого А и инверсного ?В, операндов.
Устройство переноса строится по схеме, приведенной на рис. 4.2.2, так как выражение (4.2.7) переноса в (
i
+ 1)–й разряд для АЛУ имеет такой же вид как для сумматора. Снимаемые с его выходов сигналы
G
,
P
предназначены для организации группового параллельного переноса при построении 8–, 12–, 16–разрядных АЛУ на основе рассматриваемого 4–разрядного АЛУ. 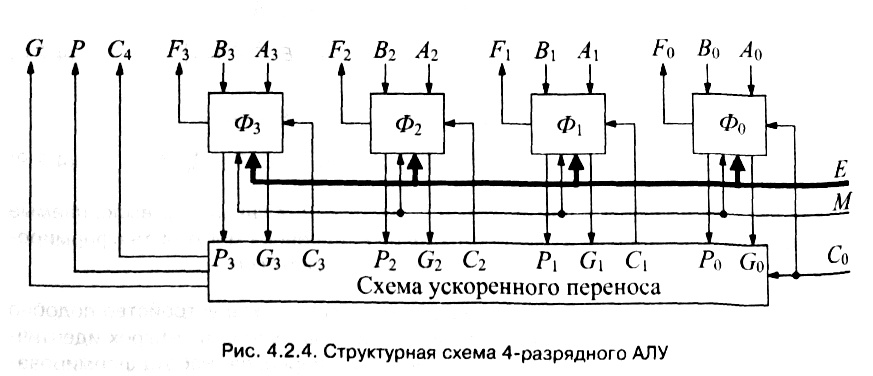
Структурная схема 4–разрядного АЛУ изображена на рис. 4.2.4. Условное графическое обозначение 4–разрядного АЛУ приведено на рис. 4.2.5. 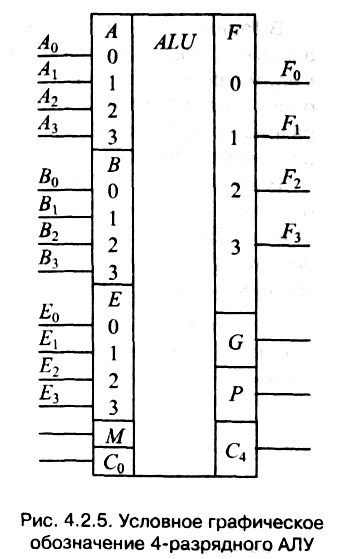

 onetwoclick.ru
onetwoclick.ru