К вопросу о моделировании процессов сепарации влаги в парогенераторе

Мечтаева М.Н. (ИГЭУ, Иваново, Россия)

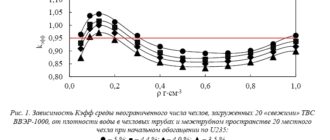
Ядерная энергетическая установка (ЯЭУ) включает в свой состав большое количество теплообменного оборудования. Важнейшим компонентом энергоблоков с реакторами типа ВВЭР являются горизонтальные парогенераторы (ПГ), которые связывают первый и второй контуры (рис. 1), и поэтому выполняют исключительно ответственную роль.

Парогенератор представляет собой специальное теплообменное устройство, предназначенной для генерации рабочего пара необходимых параметров [10]. Рабочий пар производится из питательной воды парогенераторов, которая получает теплоту от теплоносителя реактора.

Одним из важнейших эксплуатационных параметров ПГ является качество производимого пара. Среди контролируемых показателей качества пара одни свидетельствуют о чистоте самого пара, а другие (косвенно) – о чистоте конденсата.

Чистоту конденсата характеризует содержание в паре свободной углекислоты, которое не должно превышать 2 мг/кг. Для ее удаления необходимо контролировать поступление химических соединений в питательную воду с подсосом охлаждающей воды в конденсаторе турбины. Достижение требуемой величины данного параметра, не может быть осуществлено улучшением чистоты собственно пара и от самого парогенератора не зависит.

Целесообразно нормировать влажность пара. Продукты коррозии находятся во влаге в виде крупно- или мелкодисперсном состоянии, их отложение более вероятны с увеличением концентрации продуктов коррозии в уносимой влаге и от величины влажности насыщенного пара.

Влажность нормируется и не должна превышать проектной величины 0,2 % по массе на выходе из ПГ. Увеличение влажности пара на 1 % ведет за собой снижение внутреннего относительного КПД турбины на 1 %.

Если не принимать никаких мер по удалению капель влаги из генерируемого пара, возникнет недопустимо большая эрозия лопаток. В паровых турбинах ударному эрозионному износу подвержены рабочие лопатки последних и предпоследних ступеней конденсационных турбин. Поэтому обеспечение низкой влажности пара на выходе из парогенератора является важной задачей в теплоэнергетике.

Для обеспечения жестких требований к влажности пара, предъявляемых к ПГ АЭС, необходима модернизация и оптимизация конструкции пароприемных устройств ПГ [1]. Большинство исследований по модернизации и оптимизации конструкции ПГ носят опытно-экспериментальный характер, что сопряжено со значительными финансовыми и временными затратами. Понятно, что такой метод неприменим для исследований и обоснования работоспособности парогенераторов и барабансепараторов современных АЭС, находящихся в стадии проектирования.

Исходя из всего вышеперечисленного, целесообразным является проведение математического моделирования работы парогенератора и его основных узлов. Результаты расчетов, полученные с помощью ЭВМ, помогут спрогнозировать эффективность сепарации в парогенераторе и оценить вынос капельной влаги за его пределы.

Целью данной работы является создание в программной системе конечноэлементного анализа ANSYS Fluent 19.1 полноценной математической модели для изучения процессов сепарации влажного пара, происходящих в паровом объеме парогенератора ПГВ–1000М [6].

Данная модель должна иметь возможность:

определения влияния гравитационной сепарации на содержание влаги в паровом потоке;
построения зависимости влажности пара от высоты парового пространства;
оценки влияния ППДЛ на выравнивание поля скоростей в паровом объеме;
а также визуализации траекторий потоков пара и капель влаги.

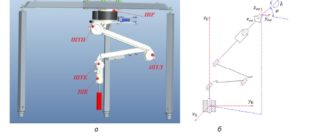
В качестве объекта исследования был взят парогенератор ПГВ–1000М эксплуатируемый на 5 ЭБ Новоронежской АЭС (рис.2). При нормальных условиях эксплуатации паропроизводительность этого парогенератора составляет от 408 кг/с до 43 кг/с при давлении 6,27 МПа и температуре 278,5 °С.

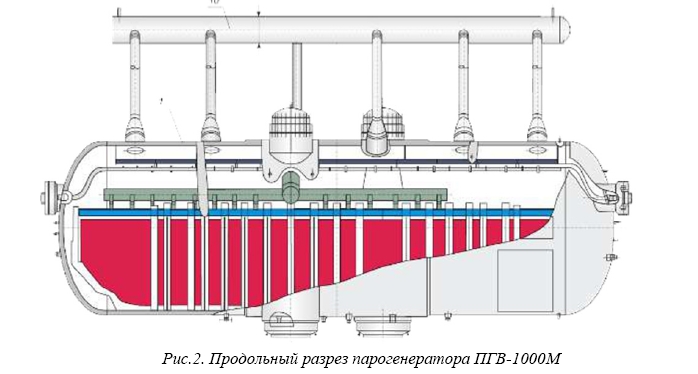
Рис.2. Продольный разрез парогенератора ПГВ-1000М

В ходе проведения работы по инженерным чертежам была воспроизведена расчетная область. Она включает в себя паровой объем парогенератора, ограниченный поверхностью зеркала испарения расположенной на уровне 2550 мм, поверхностями «горячего» и «холодного» коллекторов, корпусом самого парогенератора, стенками пароотводящих патрубков и сечением парового коллектора (рис.3).

Рис. 3. Расчетная область модели парогенератора ПГВ-1000М

На входном граничном условии задан профиль паровой нагрузки (см. таблицу) для нормальных условий эксплуатации парогенератора, который представлен в таблице. На выходе дан перепад давления парового пространства, который составляет 0,1МПа.

Таблица

Паропроизводительность участков зеркала испарения, кг/с

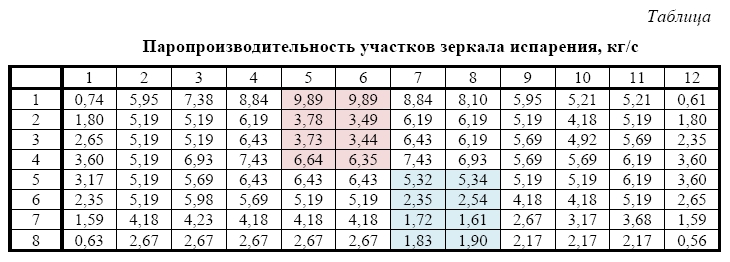
В области «горячего» коллектора наблюдается более интенсивное парообразование, что объясняется высокими температурами т/н 1-го контура.

Имеет место перекос из-за разницы в тепловых нагрузках с «горячей» и «холодной» стороны в ПГ, из-за чего возникают перекосы уровня, паросодержания и скорости движения пара [8].

ANSYS для решения поставленной задачи применяет метод конечных элементов [11]. Суть метода заключается в том, что расчетная область разбивается на некоторое количество малых, но конечных по размерам элементов (рис. 4), и для каждого элемента численным методом решаются дифференциальные уравнения с частными производными.

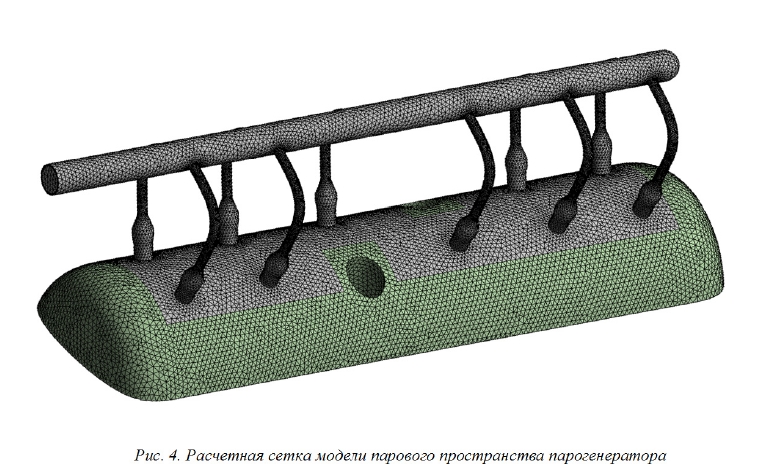
Рис. 4. Расчетная сетка модели парового пространства парогенератора

Поток пара моделируем как сплошную среду, решая уравнения Навье–Стокса.

Эта система уравнений называется уравнениями Навье–Стокса для течения вязкой сжимаемой жидкости с переменными свойствами.

Вместе с уравнением неразрывности уравнения Навье–Стокса образуют замкнутую систему:

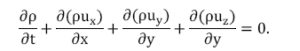
Слагаемые левой части системы уравнений определяют изменение свойств потока жидкости (газа) во времени и количества движения жидкой частицы. Слагаемые правой части уравнений определяют действие массовых сил, сил давления и сил вязкости. Таким образом, уравнения рассматриваются как баланс сил инерции (левая часть), массовых сил, сил давления и вязкости (правая часть), действующих на жидкую частицу.

Точное решение уравнений Навье–Стокса очень затратно для ЭВМ. ANSYS Fluent 19.1 [11] рассчитывает уравнения Навье–Стокса, осредненные по Рейнольдсу.

Решать эти уравнения необходимо совместно с условиями однозначности (начальные и граничные условия), представленными выше.

Капли влаги моделируем как дискретную фазу в виде сферических частиц, рассеянных в непрерывной фазе (паровой поток), с помощью DPM (Discrete Phase Model). ANSYS Fluent [11] может вычислить траектории этих дискретных фазовых объектов, а также тепломассоперенос в/из них. Расчет дискретной фазовой траектории осуществляется в Лагранжевой формулировке, включающей дискретную фазовую инерцию, гидродинамическое сопротивление и силу тяжести, как для стационарных, так и для нестационарных течений.

Лагранжева дискретная фазовая модель в ANSYS Fluent следует подходу Эйлера–Лагранжа. Пар рассматривается как сплошная среда путем решения уравнений Навье–Стокса, в то время как дисперсная фаза решается путем отслеживания большого количества капель через расчетное поле потока. Дисперсная фаза может обмениваться импульсом, массой и энергией с жидкой фазой. Этот подход значительно упрощается, когда взаимодействиями капель дискретной фазы между собой можно пренебречь.

ANSYS Fluent предсказывает траекторию дискретной фазовой частицы (или капли) путем интегрирования баланса сил на частице, который записывается в Лагранжевой системе отсчета. Этот баланс сил приравнивает инерцию частицы к силам, действующим на частицу, и может быть записан как:

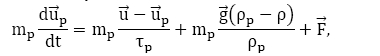
m – масса частицы (капли); u– скорость газовой фазы; u?– скорость капли; ?,? – плотность газа и капель соответственно; F – дополнительные силы; m? – сила сопротивления; ??– время релаксации капли.

Время релаксации определяется как:

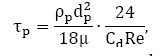
u– молекулярная вязкость жидкости; d?– диаметр капли; Re– число Рейнольдса ; Cd– коэффициент сопротивления.

Число Рейнольдса определяется как:

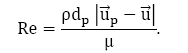
Моделирование сепарации влаги в паровом объеме ПГВ–1000 включает в себя следующие этапы:

построение геометрии расчетной области;
построение конечно–элементной сетки;
создание материалов;
установка начальных параметров рабочего тела и граничных условий, подключение необходимых уравнений для решения задачи;
запуск процесса решения;
просмотр результатов расчета.

При решении поставленной задачи принимались допущения:

поверхность зеркала испарения ровная;
капли не оказывают влияния на движение пара;
взаимодействием между каплями пренебрегается;
капли имеют сферическую форму;
распада капель не происходит.

В ходе проведенных расчетов были получены и проанализированы следующие результаты:

определено распределение абсолютного давления в паровом пространстве ПГ;
проведена оценка влияния пароприемного дырчатого листа (ППДЛ) на выравнивание скорости посредством представления распределения скоростей под ППДЛ и над ППДЛ;
визуализированы траектории потока генерируемого пара и капель влаги диаметром 10–500 мкм;
представлено распределение концентрации влаги по паровому объему ПГ.

Ниже представлены результаты расчетов полей абсолютного давления в паровом пространстве парогенератора (рис. 5) и скорости пара (рис.6) в парогенераторе. Данное распределение соответствует поведению процессов, протекающих в парогенераторе [9].

Особенностью является то, что скорости выхода пара с поверхности зеркала испарения преобладают в области горячего коллектора, что вполне логично. Наблюдается значительная неравномерность нагрузки зеркала испарения.

Рис. 5. Распределение абсолютного давления в паровом объеме парогенератора

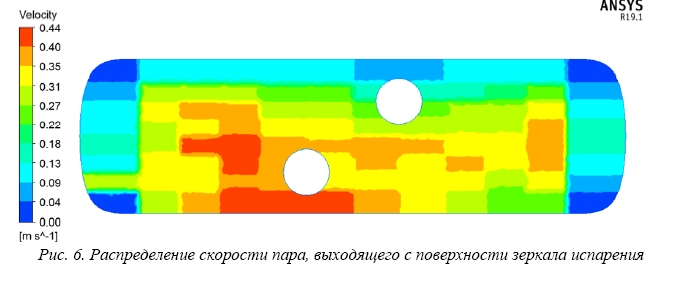
Рис. 6. Распределение скорости пара, выходящего с поверхности зеркала испарения

Распределение, изображенное на рис. 6, соответствует логике физических процессов, происходящий в парогенераторе, в области горячего коллектора преобладают скорости с наибольшими значениями. В то же время, скорости не превышают требуемого значения.

Оценку влияния ППДЛ на выравнивание скорости визуализируем посредством представления распределения скоростей под ППДЛ и над ППДЛ.

Рис. 7. Распределение скорости под ППДЛ

Рис. 8. Распределение скорости над ППДЛ

Визуальная оценка представленных результатов говорит о необходимости переменной перфорации ППДЛ, для более равномерной подачи пара в паропровод.

Результат визуализации траектории потока пара представлен на рисунке 9.

Анализ результатов расчета определяет некоторые особенности течения пара в паровом объеме парогенератора:

вихревое движение пара в пристеночной области ППДЛ и эллиптических обечаек;
вихревое движение пара в зоне коллекторов теплоносителя первого контура и стенок ППДЛ;
закручивание потока пара в шарообразной области паропровода;
закручивание потока на в ходе в коллекторы отбора пара.

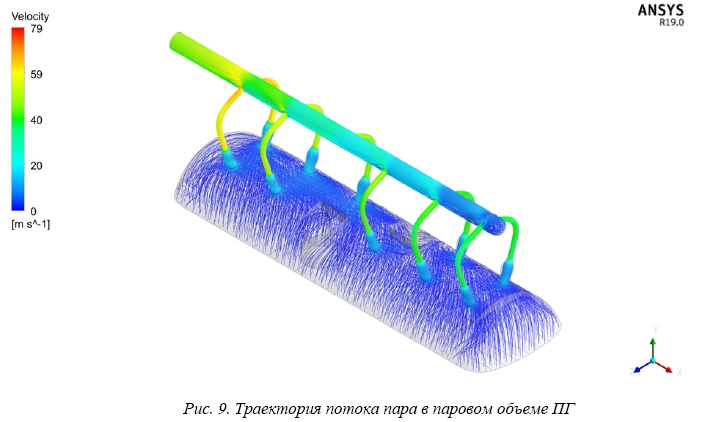
Рис. 9. Траектория потока пара в паровом объеме ПГ

Результаты расчетов траектории капель влаги представлены на рисунках 10–16.

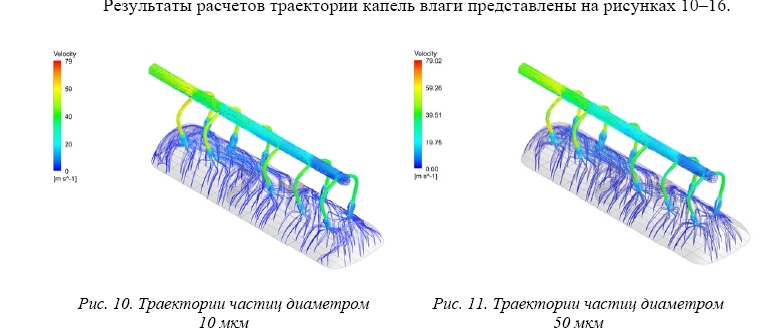
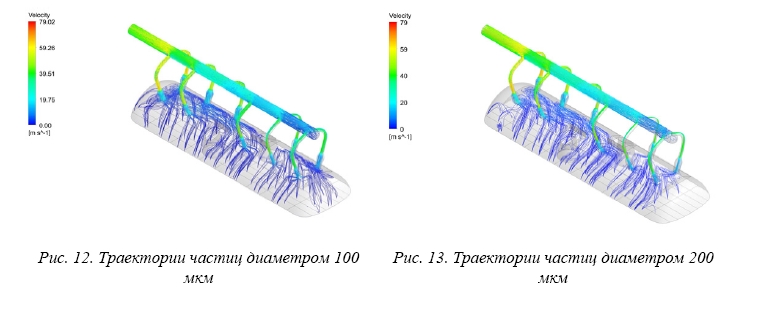
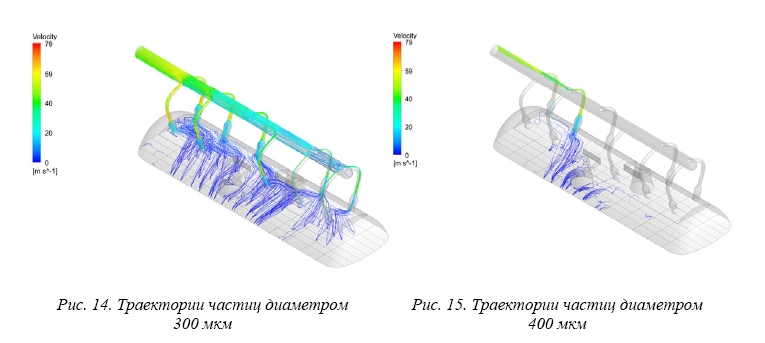
Рис. 16. Траектории частиц диаметром 500 мкм

Капли влаги диаметром 10, 50, 100, 200 мкм имеют схожие траектории движения, но отличаются количеством частиц, попавших в паропровод.

В областях, где скорость выхода пара с поверхности зеркала испарения не велика (в зонах эллиптических обечаек) капли диаметром 200 и 300 мкм оседают на поверхность зеркала испарения.

Отличительная черта капель диаметром 400 мкм связана с их выбросом в один коллектор. Это связано с тем, что входная скорость пара в области горячего коллектора высокая (выше скорости витания), капельная влага подхватывается установившимся потоком пара и вылетает в коллектор. В областях с относительно низкой скоростью пара, скорость витания капель больше, поэтому они оседают обратно на поверхность зеркала испарения.

Капли диаметром 500 мкм выносятся паром с поверхности зеркала испарения лишь в зонах с высокой скоростью пара и практически сразу возвращаются обратно.

Результаты расчетов распределения концентрации влаги в паре представлены на рисунке 17.

Рис.17. Концентрация влаги в паровом объеме парогенератора

Анализ результатов расчета показывает, что характер процессов, которые протекают в паровом объеме парогенератора, соответствует теоретическим выкладкам [9].

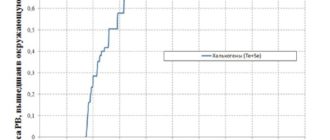
Для оценки достоверности полученных результатов, было сделано сравнение экспериментальной сепарационной характеристики парогенератора ПГВ–1000М 5-го энергоблока Нововоронежской АЭС со значением влажности пара, полученной расчетным путем на одном и том же уровне зеркала испарения. Расчетное значение влажности составляет 0,184 % (отмечено красной точкой на рис. 18.).

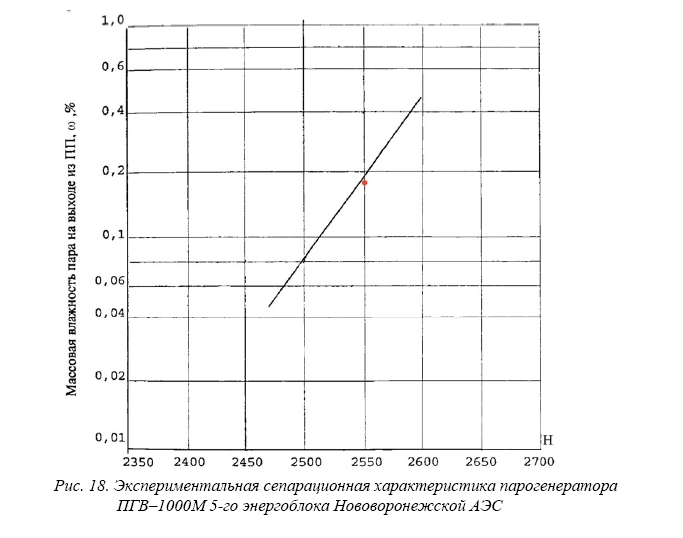
Рис. 18. Экспериментальная сепарационная характеристика парогенератора ПГВ–1000М 5-го энергоблока Нововоронежской АЭС

Была определена относительная погрешность расчетов:

Созданная математическая модель верифицирована и может быть внедрена в производство на этапе моделирования парогенераторов и барабан-сепараторов АЭС, котлов-парогенераторов ТЭС.

Перспективы дальнейшего исследования проблемы могут быть отражены в более детальном изучении:

влияния поверхности зеркала испарения на влажность пара в паровом объеме парогенератора [4];
влияния количества паропроводов отвода пара на протекание процессов в паровом объеме парогенератора;
влияния переменной перфорации погруженного дырчатого листа (ПДЛ) и ППДЛ на паровую нагрузку [4].

Список литературы

Агеев А.Г., Карасев В.Б. и др. Сепарационные устройства АЭС. – М.: Энергоиздат, 1982. – 169 с.
Кутателадзе С.С., Стырикович М.А. Гидродинамика газожидкостных систем – М.: Энергия, 1976. – 296 с.
Маргулова Т.Х. Расчет и проектирование парогенераторов атомных электростанций: Учебное пособие для вузов / – Л. : ГЭИ, 1962 . – 144 с.
Мечтаева М.Н., Горбунов В.А. К вопросу о моделировании работы парогенератора. – Материалы международной научно-технической конференции «Состояние и перспективы развития электро- и теплотехнологии» (XIX Бенардосовские чтения), Том II, Иваново, 2017.
Мечтаева М.Н., Горбунов В.А. К вопросу о моделировании процессов сепарации влаги в парогенераторе. – Материалы международной научно-технической конференции «Состояние и перспективы развития электро- и теплотехнологии» (XX Бенардосовские чтения), Том II, Иваново, 2019.
Нефёдов Е.Д. Дипломная работа: Моделирование процессов сепарации влаги в парогенераторе на ЭБ ВВЭР-1000 , ИГЭУ, 2019.
Ривкин С.Л., Александров А.А. Теплофизические свойства воды и водяного пара. – М.: Энергия, 1980. – 424 с., ил.
Теплогидродинамические процессы в реакторах и парогенераторах : Учеб. пособие / [В. М. Боришанский, Т. В. Заблоцкая, П. Л. Магидей, А. Я. Благовещенский]. – Л.: ЛПИ, 1984. – 80 с. : ил.; 22 см.
Трунов Н.Б., Логвинов С.А., Драгунов Ю.Г. Гидродинамические и технологические процессы в парогенераторах АЭС с ВВЭР. – М.: Энергоатомиздат, 2001. – 316 с.
Федоров Л.Ф., Рассохин Н.Г. Процессы генерации пара на атомных электростанциях/ – М., Энергоатомиздат, 1985, 288 с.
Справочник ANSYS Help.