Алексеев П.В., Лоскутов О.Д., Тутнов А.А. (НИЦ «Курчатовский институт», Москва, Россия)
Вероятностный анализ безопасности (ВАБ) является современным подходом к обоснованию безопасности эксплуатации реакторных установок (РУ). Главным образом, ВАБ сводится к расчету частоты повреждений активной зоны в результате того или иного нарушения эксплуатации. ВАБ в этом случае представляет собой математическое моделирование конкретного энергоблока и последовательное рассмотрение цепочек (деревьев) событий и отказов, которые могут привести к реализации нежелательного события (аварии). Такое рассмотрение основывается на базе данных по статистике отказов оборудования, влияющего на безопасность, и по надежности оборудования и оперативного персонала. Периодическое выполнение ВАБ сопровождается совершенствованием модели энергоблока и методики анализов.
Анализ строится на учете инициирующих событий, признаваемых возможными. Одной из возможных причин отказов элементов оборудования РУ, находящегося под давлением теплоносителя, является разгерметизация трубопроводов и корпусных элементов первого и второго контуров по причине образования течи или разрыва по основному металлу или сварным швам. Статистика таких отказов, как правило, недостаточна для количественной оценки надежности оборудования, требуемой при выполнении ВАБ. В этом случае, основным способом оценки вероятности отказа оборудования РУ и, соответственно, анализа частот исходных событий, необходимых для ВАБ, является вероятностный анализ разрушения (ВАР). По существу ВАР является расчетом на прочность трубопроводов и корпусов, который проводится при вероятностном задании ряда исходных данных.
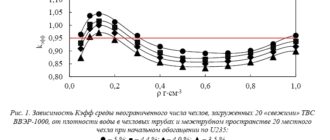
Целью данной работы является описание одной из возможных методик для ВАР корпуса главного циркуляционного насосного агрегата (ГЦНА), позволяющей получить количественную оценку надежность данного элемента конструкции. Полученные результаты представляют собой вероятность возникновения течей различной интенсивности или крупномасштабного разрушения сосуда давления. На рис. 1 представлена схема корпуса ГЦНА в разрезе.
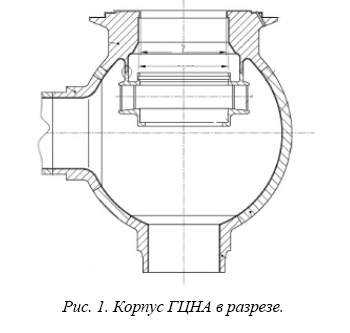
Рис. 1. Корпус ГЦНА в разрезе.
Анализ надежности данного элемента конструкции осуществляется в два этапа. Рассмотрим каждый из них подробнее.
На первом этапе проводится расчет напряженно-деформированного состояния (НДС) нестационарных полей температуры и корпуса. Расчет осуществляется с использованием специальных или универсальных программных средств, предназначенных для пространственных прочностных расчетов конструкций (УЗОР-1, ANSYS и др.). На основе этих расчетов формируется библиотека распределений напряжений и температур корпуса для различных проектных режимов его работы, а также остаточных технологических напряжений. На данном этапе расчетная модель представляет собой сложный толстостенный объект, состоящий и множества элементарных объемов и детально учитывающий все геометрические особенности реального корпуса ГЦНА. Подобная степень детализации, при современном развитии вычислительной техники, позволяет точно установить наиболее нагруженные зоны объекта, и, путем корректировки исходных данных для последующих расчетов, сделать окончательную оценку более точной.
Следующим этапом осуществляется окончательный расчет вероятности возникновения течи или крупномасштабного разрушения корпуса. Рассмотрим эту методику более подробно.
Данный этап выполняется по следующему алгоритму:
- корректируется заданное начальное распределение дефектов материала с учетом вероятности их пропуска при неразрушающем контроле и возможности устранения (ремонта) дефектов с размерами, превышающими допустимые по техническим условиям;
- выполняется моделирование процессов зарождения и слияния микротрещин в процессе эксплуатации;
- выполняется моделирование докритического роста трещин в процессе эксплуатации;
- выполняется моделирование возможных вариантов развития трещины и расчет вероятности реализации приведенных сценариев;
- распределение трещин по числу и размерам корректируется с учетом их зарождения и роста;
- рассчитываются распределения вероятности критических размеров трещин при хрупком, хрупко-вязком и вязком механизмах разрушении;
- помимо докритического подрастания, учитывается возможность старта и остановки трещин при заданных вероятностным образом значениях критических параметров для хрупкого, хрупко-вязкого и вязкого механизмов разрушения.
- выполняется расчет распределения вероятности максимальных и минимальных значений площади раскрытия сквозной трещины, эквивалентного диаметра и интенсивности течи.
Исходными данными для этих расчетов, помимо полей напряжений и температуры, являются: характеристики чувствительности и точности дефектоскопического контроля, параметры дефектности в исследуемом объекте (число и размеры дефектов), физико-механические и прочностные свойства основного металла и сварных швов, параметры водно-химического режима теплоносителя, история нагружения объекта в процессе эксплуатации. Параметры дефектности материала задаются в виде статистических распределений. Прочностные свойства материала задаются таблично, однако, на этапе расчета критических размеров дефектов, также приводятся к вероятностному виду. Это позволяет учитывать возможные погрешности при конечных оценках вероятности возникновения течи и разрушения.
Существуют различные статистические расчетные методики, позволяющие проводить ВАР сосудов давления реакторных установок (РУ). Например, широко распространены методики, реализующие метод Монте-Карло, как способ моделирования случайных событий. [1] Недостатком данного метода является потребность в независимом генераторе случайных величин. Количество качественно различных алгоритмов получения последовательностей случайных чисел, в настоящее время, сильно ограничено. Ввиду этого, многие параметры, используемые при расчете, формируются по одному и тому же алгоритму, что, по сути, делает их взаимозависимыми.
В основе предлагаемой методики лежит метод пересечения статистических величин. Согласно методу, вероятность возникновения одной сквозной трещины с длиной l диапазона от до вычисляется как пересечение распределений двух случайных независимых величин:
![]()
где , Рх(хС), – плотность вероятности распределения размеров трещины по направлению в глубину (параметр x) и в длину (параметр С) рассматриваемой конструкции; Fx кр(хС) – вероятность события, при котором критический размер дефекта в глубину кр, при заданной длине С, окажется меньше, чем величина x. Под критическим понимается дефект с размерами кр и С, при которых происходит неконтролируемый подрост трещины на всю толщину без лавинного роста в длину. Аналогично вычисляется вероятность старта сквозной трещины в продольном направлении и крупномасштабного разрушения.
Формула (1) для вычисления вероятности возникновения течи соответствует случаю когда в рассматриваемом объеме металла только одна трещина, размеры которой характеризуются случайным двумерным статистическим распределением с плотностью вероятности ,. На самом деле, трещины могут зарождаться в различных перемычках независимо. Если по результатам неразрушающего контроля трещин окажется больше, например, n, то в соответствии с концепцией слабейшего звена вероятность разрушения запишется в виде:
![]()
Поскольку число трещин в рассматриваемом объеме также является случайной величиной (заданной дискретным распределением ), то полную вероятность возникновения течи можно записать в виде
![]()
Здесь Pn (ni) описывается законом Пуассона.
Более подробно, данная методика изложена в [2]. Особенностью расчетов корпуса ГЦНА является его геометрия. Предлагаемая методика учитывает требования актуальных руководящих документов, каких как [3–6], и может быть использована для проведения практических расчетов в рамках обоснования надежности оборудования АЭС. В качестве примера, рассмотрим результаты расчетов вероятности разрушения и результаты расчета вероятности образования течи и вероятности разрыва (крупномасштабного разрушения) сферического корпуса ГЦНА-1391 за проектный срок эксплуатации. Подробно описание исходных данных и результатов приведено в [7].
Особенностью в данной работе было то, что для определения размеров дефектов была использована методика «нулевой дефектности» материала, т.е. по результатам неразрушающего контроля (НК) дефекты в металле обнаружены не были. В этом случае, распределения характеристик дефектности (глубины, длины и числа трещин), рассчитывались с использованием данных о выявляемости дефектов для капиллярного и радиографического контроля, которые приведены в таблице 1.
Был рассмотрен также вариант выявляемости дефектов, идентичный, представленному в таблице 1, но при котором выявляемость 80 % соответствовала глубине дефекта 15 мм, а не 75 мм (таблица 2).
Таблица 1
Вероятность обнаружения дефектов для капиллярного и радиографического контроля
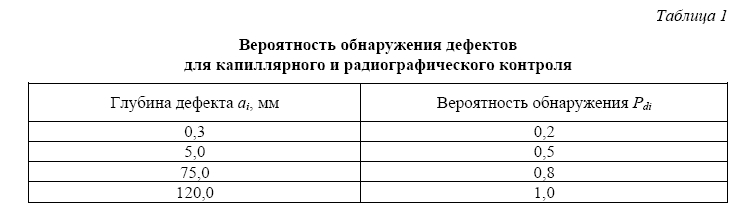
Таблица 2
Вероятность обнаружения дефектов разной глубины
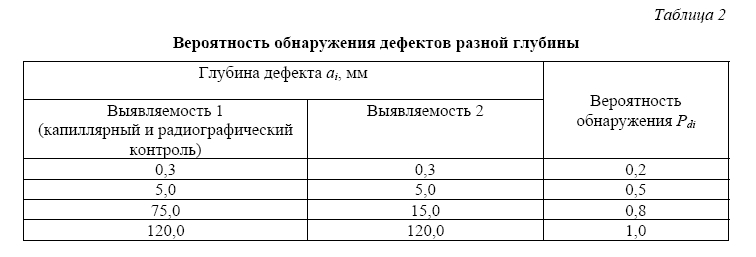
Выявляемость 1 (первый столбец табл. 2) соответствует нулевой дефектности № 1. Выявляемость 2 (второй столбец табл. 2) соответствует нулевой дефектности № 2.
Рассмотрим методику расчета распределения глубины, длины и числа дефектов, не выявленных при НК.
Задается априорная функция распределения размера дефекта (глубины) ( ) F a в интервале (0,h), где h – толщина стенки оборудования РУ (сосуда давления или трубопровода). Определяется вероятность того, что дефект, глубина которого находится в интервале ? a a da ?[ , , при НК не будет обнаружен:

Определяется вероятность необнаружения (пропуска) дефекта, размер которого находится в интервале (0,a100):
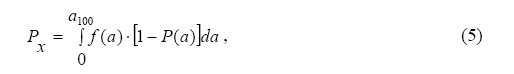
где а100 – минимальная глубина дефектов, обнаруживаемых со 100 % вероятностью, в частности возможно а100 = h.
Из того факта, что при НК дефект не обнаружен, следует:

где f0 (a) – плотность апостериорного распределения глубины необнаруженных дефектов.
Поскольку x P есть полная вероятность необнаружения дефекта при данном методе НК, в соответствии с формулой Байеса получим [8]:

Априорные функции распределения длины и глубины дефекта связаны соотношением:

где с – полудлина дефекта, ограниченная интервалом (0,k·a100), k >= 1 – коэффициент формы дефекта.
Тогда апостериорная плотность распределения длины необнаруженных дефектов определяется как

Распределение числа дефектов в элементе определяется следующим образом. Предполагается, что обнаружение дефектов при НК есть независимые случайные события, то есть вероятность обнаружения дефекта не зависит от того, обнаружены или нет другие дефекты. В этом случае вероятность того, что пропущенное число дефектов в объекте равно или больше т, рассчитывается как вероятность реализации т событий при т независимых испытаниях, причем события имеют одинаковую вероятность x P :


Из факта, что при НК не был обнаружен ни один дефект больше браковочного уровня, следует, что xm P есть вероятность того, что число дефектов в объекте равно m.
В частности, матожидание числа пропущенных дефектов в объекте:

Таким образом, все статистические характеристики нулевой дефектности, необходимые для расчета вероятности разрушения в рамках методики, а именно распределения глубины, длины и числа дефектов, определены.
Очевидно, характеристики распределения нулевой дефектности зависят от априорного распределения размера дефектов и от зависимости вероятности обнаружения дефекта от его размеров для примененного метода НК.
Поскольку при задании априорного распределения присутствует элемент субъективизма, было проанализировано влияние параметров априорного распределения на результат расчета вероятности разрушения объекта. Было показано, что смещение априорного распределения в сторону увеличения глубины дефектов сдвигает в сторону уменьшения распределение числа дефектов. Эти два фактора имеют противоположную направленность на вероятность разрушения, что снижает влияние матожидания априорного распределения на конечный результат оценки вероятности разрушения [9].
В случае, если при эксплуатационном контроле конкретного объекта обнаруживаются один или несколько дефектов, этого недостаточно для получения статистических характеристик дефектности. Тогда рассчитывается вероятность разрушения от каждого из обнаруженных дефектов Pi>0 с учетом конкретных размеров этих дефектов. Рассчитывается вероятность разрушения при нулевой дефектности P0 по описанному выше алгоритму. Полная вероятность разрушения рассчитывается по формуле:

Если периодический эксплуатационный контроль не обнаруживает новых дефектов, то при проведении вероятностного анализа разрушения на рассматриваемом этапе в качестве априорных распределений можно использовать апостериорные функции распределения глубины и длины необнаруженных дефектов, полученные на предыдущем этапе.
Распределения размеров и числа не выявленных при НК дефектов (нулевая дефектность) определялись по описанной выше методике с использованием априорного равномерного распределения размеров необнаруженных дефектов

и кусочно-линейной зависимости вероятности обнаружения дефектов от глубины

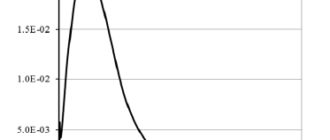
где h – толщина стенки корпуса, ai и Pdi характеристики выявляемости дефектов, приведенные в таблице 2. Результаты расчетов представлены графически на рис. 2,3

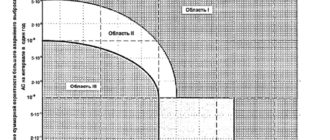
Рис. 2. Вероятность течи разных ДУ в сварных швах корпуса ГЦНА-1391 при нулевой дефектности № 1 (кривая 1) и нулевой дефектности № 2 (кривая 2) при проектных режимах эксплуатации
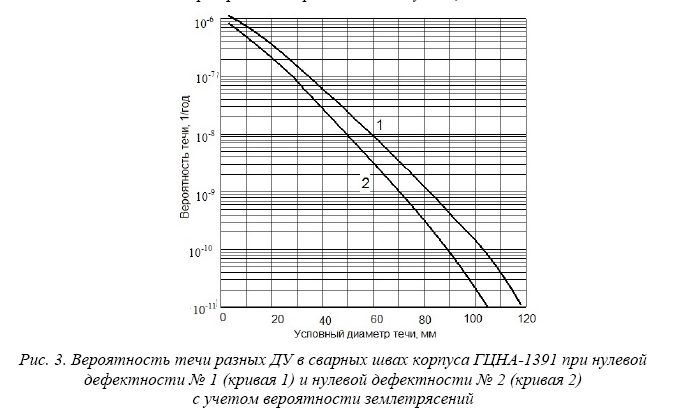
Рис. 3. Вероятность течи разных ДУ в сварных швах корпуса ГЦНА-1391 при нулевой дефектности № 1 (кривая 1) и нулевой дефектности № 2 (кривая 2) с учетом вероятности землетрясений
Заключение
Таким образом, в рамках данной статьи, была предложена методика, позволяющая проводить ВАР корпусов ГЦНА, описана методика расчета распределений дефектности материала в случае, когда средствами НК дефекты не были обнаружены, а также представлены результаты применения данной методики на практике. Стоит отметить, что, при учете геометрических особенностей, данный подход может быть применен практически для любых толстостенных сосудов давления РУ.
Список литературы
- Александров А.Е., Тюрин А.В., Киселев М.Н. Анализ вероятности разрушения корпуса реактора ВВЭР с использованием эффективной расчетной модели. – ВАНТ. Серия: Физика ядерных реакторов, 2015, вып. 3.
- Алексеев П.В. Расчетное моделирование процессов накопления повреждений коллектора парогенератора ПГВ-1000 в вероятностной постановке: дис. … канд. техн. наук: 05.14.03. – НИЦ «Курчатовский институт», Москва, 2014 – 164 с.
- Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок (ПНАЭ Г-7-002-86) / Госатомэнергонадзор СССР. – М.: Энергоатомиздат, 1989. – 525 с.
- Руководство по расчету на прочность оборудования и трубопроводов реакторных установок РБМК и ВВЭР на стадии эксплуатации. РД ЭО 0330-01. Москва, 2001.
- НП-001-15. Общие положения обеспечения безопасности атомных станций.
- Правила составления расчетных схем и определения параметров нагруженности элементов конструкций с выявленными дефектами: методические рекомендации. МР 125-02-95 /НПО «ЦНИИТМАШ», НИКИЭТ. – М.,1995. – 52 с.
- ВВЭР-ТОИ. Установка реакторная В-510. Расчетный анализ вероятности крупномасштабного разрушения и возникновения течей с эквивалентным диаметром более Ду 43 в корпусе ГЦНА. Инв. № 32.1/50– 311. РНЦ «Курчатовский институт». 2011.
- Вентцель Е.С. Теория вероятностей. М.: Наука, 2002.
- Голубева О.В., Лоскутов О.Д., Тутнов А.А. Задание характеристик дефектности материала для расчетов вероятности разрушения при отсутствии статистических данных о дефектности. Сборник докладов. Методы и программное обеспечение расчетов на прочность // Материалы шестой российской конференции, 4–8 октября 2010 г., Геленджик/М, с. 241– 248.

 onetwoclick.ru
onetwoclick.ru