В том случае, когда наблюдения об изменении технического состояния устройства не имеют достаточного обоснования, связанные с этим явления приобретают характер случайного процесса. Чем меньше имеется информации о физическом механизме происходящих процессов, тем менее предсказуемым является такой процесс. Другая сложность в решении задач прогнозирования является в индивидуальном характере изменения параметров устройств, связанных как с первоначальным разбросом параметров комплектующих элементов, так и с погрешностями сборки, занимающими в настоящее время большое место, а также с другими факторами.
Методы группового прогнозирования базируются на результатах анализа обычных и ускоренных ресурсных испытаний, дают общую картину изменения технического состояния совокупности однотипных изделий. Применение методов фильтрации, адаптированного прогнозирования временных рядов, поиск функциональных детерминистских и стохастических зависимостей при групповом прогнозировании оправданы, но не могут быть перенесены на методы индивидуального прогнозирования, так как при этом не удается учесть специфические особенности каждого из однотипных объектов.
Для создания методов индивидуального прогнозирования наиболее приемлемым является метод моделирования с использованием уравнений изменения технического состояния. Такой подход позволяет еще на стадии проектирования анализировать различный характер поведения системы в реальных условиях.
Методы прогнозирования состояния оборудования
Рассмотрим различные методы прогнозирования, отражающие различную глубину используемой априорной информации о системе.
Адаптивный метод линейной фильтрации. Прогнозирование основано на анализе предшествующих данных и использует минимум априорной информации о модели системы, генерирующей временной ряд значений параметров, характеризующих техническое состояние. Операция линейной фильтрации заключается в вычислении взвешенной суммы предыдущих наблюдений:
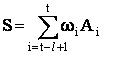 где S взвешенная средняя; i вес, приписываемый наблюдению; Ai значение параметра, характеризующее техническое состояние системы в момент i : l число наблюдений, используемое при оценке.
где S взвешенная средняя; i вес, приписываемый наблюдению; Ai значение параметра, характеризующее техническое состояние системы в момент i : l число наблюдений, используемое при оценке.
Рассматриваемая модель представляет собой авторегрессионую схему с дрейфующими коэффициентами. Частным случаем рассматриваемой системы является метод скользящих средних, который состоит в том, что все анализируемые данные используются с постоянным весом. Результат определения последних членов временного ряда используется как прогноз. При использовании экспоненциального сглаживания ![]() где a постоянная сглаживания (0< a <1).
где a постоянная сглаживания (0< a <1).
В этом методе наибольший вес имеет текущее значение, а для предыдущих наблюдений имеет место убывание весов. Прогноз ожидаемого значения временного ряда осуществляется в результате вычисления. Различные способы задания коэффициентов i определяют возможные вариации в построении фильтров. При адаптивных методах фильтрации корректировка коэффициентов i производится в процессе наблюдения временного ряда. В этом методе характеристики ряда наблюдений не измеряются, но учитываются в ходе адаптации коэффициентов i фильтра. Корректировка весов производится на основании анализа шибки прогноза, которую можно представить в виде:![]() где At+1 фактическое значение ряда наблюдений в момент времени t+1. Квадрат ошибки прогноза является квадратической функцией от весов i. Адаптация осуществляется таким образом, чтобы минимизировать l t+1.
где At+1 фактическое значение ряда наблюдений в момент времени t+1. Квадрат ошибки прогноза является квадратической функцией от весов i. Адаптация осуществляется таким образом, чтобы минимизировать l t+1.
Преимущества методов прогнозирования
Преимуществом рассмотренных и близких к ним адаптивных методов линейной фильтрации является простота, использование минимума априорной информации об объекте. Недостатком является то, что адаптируемая модель, следуя за наблюдаемым процессом, не позволяет прогнозировать (упреждать) изменение технического состояния для значительных интервалов времени и может использоваться при краткосрочных прогнозах (на один шаг).
Для анализа могут использоваться спектральные характеристики вибрации или функции параметров z(t).
Методы краткосрочного прогнозирования эффективны для сглаживания, фильтрации характеристик, по которым оценивается техническое состояние системы.
Прогнозирование процессов с детерминированными основами. Отсутствие априорной информации о характере изменения прогнозируемого параметра существенно снижает эффективность прогноза. Вместе с тем , информация о системе, полученная в результате испытаний, эксплуатации, а также информация об аналогах этих устройств, дает возможность предполагать возможный характер изменения анализируемых параметров. Например, рассматривая прогнозируемый параметр z(t) как нестационарную случайную функцию ![]() где математическое ожидание случайной функции z(t); V некоррелированные случайные величины, математическое ожидание которых равно нулю; f (t) детерминированные функции.
где математическое ожидание случайной функции z(t); V некоррелированные случайные величины, математическое ожидание которых равно нулю; f (t) детерминированные функции.
Предполагается, что вид координатных функций на участке прогнозирования не изменится по сравнению с их видом на участке наблюдения. На участке наблюдения за случайным процессом определяется вид координатных функций и коэффициенты V или V(). Этот метод, имея детерминированную основу в виде координатных функций, не требует априорного знания их вида, все необходимые данные получаются в результате наблюдения за процессом z(t) .
Рассмотренный метод может использоваться для прогнозирования изменения спектральных характеристик вибрации и флуктуаций диагностических параметров, например, амплитудных значений z(t)=A(t) , а также параметров, характеризующих изменяющиеся дефекты системы z(t)= Недостатком этого метода является необходимость анализировать большой объем статистической информации, включая определение и R(t, t) .

 onetwoclick.ru
onetwoclick.ru