Погрешности расчетов потерь электроэнергии: методы, формулы, описание

Любому расчетному методу свойственны погрешности, поэтому анализ потерь электроэнергии и особенно выбор мероприятий по их снижению должны проводиться на основе оценки интервалов неопределенности потерь. В противном случае можно зря затратить средства на установку того или иного оборудования и не получить ожидаемой отдачи, хотя расчет указывал на существенный эффект.

Обзор литературы показывает, что определение погрешностей того или иного метода расчета потерь электроэнергии часто используется лишь для качественной оценки его приемлемости. В практических же расчетах потерь результаты представляют в виде детерминированных величин и мало интересуются интервалами неопределенности их значений. Отличие погрешностей, например 2,3 % и 6,8 % никак не отражается на использовании полученного в результате расчета значения потерь.

Вместе с тем расчетные значения технических потерь являются такими же составляющими баланса электроэнергии, как и потери, обусловленными погрешностями приборов учета электроэнергии, при анализе которых используются основанные на понятии класса точности прибора интервальные оценки. Каждому методу расчета потерь также может быть поставлен в соответствие класс точности, и допустимый небаланс электроэнергии на объекте должен определяться с его учетом.

В известных исследованиях погрешностей методов расчета потерь их численные значения обычно определялись на основе сопоставления результатов расчетов для схем, рассматриваемых исследователем. Практическое использование этих погрешностей при расчете других сетей затруднено в связи с трудностями оценки отличий конкретной схемы от рассмотренных исследователем. Сделать более практичной оценку интервалов неопределенности потерь для любой конкретной схемы можно на основе анализа структуры погрешностей и выявления характеристик схем и методов расчета, которые, с одной стороны, достаточно жестко связаны с погрешностями расчета, а с другой стороны, сравнительно легко определяются для конкретной схемы.

Структура погрешностей расчета потерь электроэнергии

Погрешности расчета потерь аналитическими методами по причинам их возникновения можно разделить на две группы: методические и информационные. Первые обусловлены неполнотой информации, используемой методом (определяются влиянием на результат расчета неиспользуемой информации), вторые – неточностью (ограниченной достоверностью) используемой информации.

К методическим погрешностям относятся:

• погрешность, обусловленная неадекватностью отражения величинами ? и 2 ф k , определенными по графику суммарной нагрузки сети (?? и 2 ф k ? ), потерь в элементах сети, каждый из которых имеет свой график нагрузки с индивидуальными значениями ?i и 2 фi k (далее – погрешность неадекватности, ?на). Эта погрешность присутствует при расчете ?? и 2 ф k ? как по приближенным формулам (2.16) и (2.17), так и непосредственно по ординатам графика суммарной нагрузки сети по формулам (2.4) и (2.5);
• погрешность, обусловленная использованием параметров графиков контрольных суток для всего расчетного периода (далее – погрешность временной неоднородности графиков, 2 ?вр );
• погрешность, обусловленная использованием для расчета величин ? и 2 ф k приближенных формул (2.16) и (2.17) вместо точных формул (2.4) и (2.5) (далее – методическая погрешность приближенных формул, ?пр ).

К информационным погрешностям относятся:

• погрешность расчета потерь электроэнергии, обусловленная погрешностями данных об узловых нагрузках (далее – погрешность ?у );
• погрешность расчета ? или 2 ф k по приближенным формулам, обусловленная погрешностью используемого в этих формулах коэффициента заполнения графика нагрузки kз (далее – информационные погрешности приближенных формул, ?кз ? и ?кз k ф );
• погрешность, обусловленная неточностью задания параметров участков сети (использованием удельных сопротивлений линий, приведенных в справочниках при температуре 20 °С, погрешностями в длинах линий и т. п.).

Первые пять видов погрешностей обусловлены неточностями задания параметров нагрузок, шестая – параметров элементов схемы. Далее рассмотрены только погрешности, обусловленные нагрузками.

Методические погрешности могут иметь как случайную, так и систематическую составляющую; они могут или завышать, или занижать результат в среднем. При известной систематической погрешности метода в его расчетную формулу вводят соответствующие поправочные коэффициенты (см. гл. 2). Информационные погрешности имеют, как правило, только случайную составляющую, так как погрешности в исходной информации обычно трактуются как симметричные двухсторонние с нулевым средним значением.

Анализ погрешностей подробно рассмотрен в прил. 4. Ниже приведены полученные в прил. 4 расчетные формулы для определения вероятностных характеристик случайной величины погрешности в каждом конкретном расчете потерь. Необходимо еще раз обратить внимание читателя на то, что определить конкретное значение погрешности проведенного расчета нельзя. Если бы это было возможно, то мы получили бы точное значение потерь. Можно лишь правильно определить интервал неопределенности потерь, то есть утверждать, что действительные (не известные нам) потери находятся в интервале, например, (127,3 ± 6,1 %) тыс. кВт·ч. То есть с вероятностью 0,95 они не ниже 119,5 тыс. кВт·ч и не выше 135,1 тыс. кВт·ч. Целью является определение диапазона возможного отклонения действительных потерь от их расчетного значения для конкретного расчета, то есть обеспечение возможности утверждать, что он составляет не 10 % и не 3 %, а именно 6,1 %.

В различных практических задачах может использоваться как нижняя, так и верхняя граница интервала неопределенности. Эти граничные значения далее называются гарантированными. Точнее, «практически гарантированными» – имея в виду вероятность 0,95. Например, при оценке эффекта от проведения МСП целесообразно ориентироваться на нижнюю границу интервала, чтобы получить гарантированный эффект. При дискуссиях об уровне коммерческих потерь необходимо из фактических потерь вычитать верхнюю границу диапазона технических потерь, чтобы получить гарантированное (минимальное) значение коммерческих потерь и утверждать, что они не ниже этого значения, так как все возможные погрешности расчетов технических потерь уже учтены.

Далее приводятся расчетные формулы для определения каждой из описанных выше составляющих погрешности и суммарной погрешности расчета, определяющей границы интервала возможных значений технических потерь.

Погрешность неадекватности интегрирующих множителей

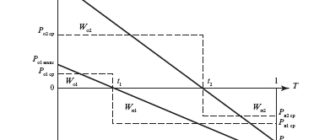
Точное значение потерь электроэнергии в сети соответствует сумме потерь, рассчитанных для каждого участка по его нагрузкам на каждой ступени графика. Такое же значение потерь будет и при расчетах методами 1 и 2 (см. п. 2.1.2), если использовать значения ?i и 2 фi k , рассчитанные для каждого участка по его графику:

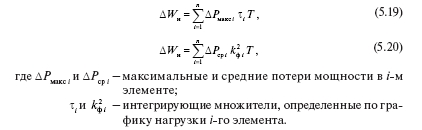
Обычно графики нагрузки элементов сети неизвестны, они появляются в результате расчета УР сети. Суммарные потери мощности в сети рассчитывают для расчетного режима (максимальной суммарной нагрузки в методе 1 и средней – в методе 2). Интегрирующие множители также определяют по графику суммарной нагрузки. При расчете режима максимальной суммарной нагрузки узловые нагрузки участвуют своими значениями, соответствующими часам максимальной суммарной нагрузки. Их собственные максимальные нагрузки могут наблюдаться в другие часы суток. Формулы для расчетных потерь электроэнергии имеют вид:

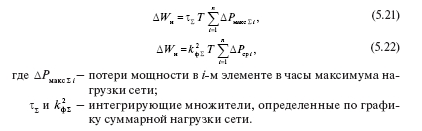
При использовании формул (5.21) и (5.22) возникают два рода погрешностей неадекватности. Погрешность первого рода обусловлена тем, что при неоднородных (различных по конфигурации) графиках нагрузки узлов график суммарной нагрузки выравнивается. Для этого графика ?? оказывается выше, а 2 ф k ? – ниже аналогичных параметров входящих в схему ветвей. Это приводит к завышению суммарных потерь при использовании метода 1 и к занижению – при использовании метода 2.

Погрешность второго рода возникает только при использовании метода 1 и обусловлена тем, что при неоднородных графиках максимальные нагрузки элементов не совпадают по времени с максимальной нагрузкой сети в целом. При этом

что приводит к занижению расчетных потерь электроэнергии при использовании метода 1.

Отрицательная погрешность второго рода будет тем больше, чем больше доля потерь в элементах с графиками нагрузки, не совпадающими с графиком суммарной нагрузки, и чем больше это несовпадение. Если, например, в режиме максимальной нагрузки сети нагрузка конкретного элемента составляла 70 % собственной максимальной нагрузки, то ?Pмакс ? i = 0,49 ?Pмакс i , и при расчете УР максимальной нагрузки сети потери мощности в данном элементе будут отражены значением, в 2 раза меньшим действительных максимальных потерь. Результирующая погрешность неадекватности в методе 1 определяется количественным соотношением этих двух разнонаправленных погрешностей для конкретной схемы.

Результирующая погрешность метода 2 определяется только погрешностью первого рода. Различие конфигураций графиков не влияет на среднюю нагрузку элемента, поэтому средние потери в элементе остаются теми же: отсутствует соотношение типа (5.23). Поэтому она всегда отрицательна.

Погрешности неадекватности первого рода в реальных условиях усиливаются еще тем обстоятельством, что график суммарной нагрузки формируется всеми потребителями, независимо от их вклада в потери. Вместе с тем более мощные потребители расположены, как правило, ближе к центрам питания и приводят к меньшим удельным потерям (так называемые «малопотерьные» потребители). Такие потребители имеют более заполненные графики нагрузки, и их нагрузки в значительной степени формируют график суммарной нагрузки.

В замкнутой сети график нагрузки каждой линии определяется режимами работы регулирующих устройств и формируется всеми узловыми нагрузками (в соответствии с коэффициентами распределения). Как правило, эти графики существенно отличаются друг от друга и от графика суммарной нагрузки сети, поэтому погрешность неадекватности для замкнутой сети имеет наибольшие значения. В радиальных линиях основная часть потерь приходится на головной участок, график нагрузки которого и является графиком суммарной нагрузки линии, и на несколько участков магистрали, графики которых близки к графику суммарной нагрузки. Поэтому погрешность неадекватности при расчетах потерь проявляется здесь слабее, чем в замкнутых сетях.

Для снижения влияния погрешностей неадекватности при расчете методами 1 и 2 используют корректирующие коэффициенты, определяемые по формулам (2.26) – (2.29). Как показано в прил. 4, погрешности неадекватности без учета корректирующих коэффициентов составляют 10,6 % и 9,3 %, а при их применении – снижаются до 3,5 % и 1,5 % соответственно.

В методе 3 суточный график суммарной нагрузки сети не используется, поэтому погрешность неадекватности на суточном интервале равна нулю.

Погрешность, обусловленная использованием параметров графиков контрольных суток для всего расчетного периода

Суточные графики отличаются не только потребляемой энергией, но и своими конфигурациями (временная неоднородность гра 2 – фиков) и, соответственно, значениями 2 ф k . Использование 2 ф k , определенного по графику дня контрольных замеров (то есть по графику одного из рабочих дней), вносит погрешность ?вр, которая может быть как положительной, так и отрицательной, и зависит от вариации значений 2 ф k графиков нагрузки в различные сутки. Эту погрешность трудно связать с каким-либо обобщенным параметром, так как определить ее можно, только рассчитав 2 ф k для всех суток расчетного периода и сопоставив их с его значением для дня контрольных замеров, что практически невозможно.

Расчеты 2 ф k для суточных графиков недельного интервала, проведенные для предприятий различных отраслей, показали, что эта погрешность колеблется в интервале 0,5–2,5 %. Для обобщенного анализа можно принять эту погрешность равной 1,5 %. Этот вид погрешности проявляется во всех методах.

Методическая погрешность приближенных формул

Методическую погрешность приближенных формул (2.16) и (2.17) определяют по формулам (прил. 1), %:

Погрешность расчета потерь мощности, обусловленная погрешностями данных об узловых нагрузках

Известно, что сумма полученных по контрольным замерам нагрузок узлов в конкретный интервал времени часто существенно отличается от суммарной нагрузки сети в целом. В связи с этим применяются процедуры балансировки нагрузок узлов и суммарной нагрузки (см. п. 2.1.6). Очевидно, что режим, полученный таким образом (сбалансированный режим), отличается от неизвестного фактического режима, хотя и удовлетворяет условию баланса.

При наличии экспертной оценки погрешности нагрузки в каждом узле ?н i , %, погрешность в потерях мощности, рассчитанных для сбалансированного режима ?у. сб , %, определяют по формуле (прил. 4)

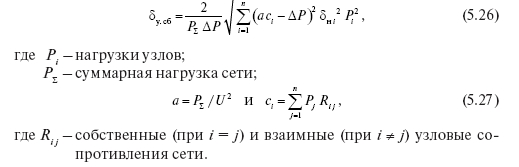
При расчете потерь в радиальных сетях 35–110 кВ суммарная нагрузка сети может быть неизвестна (отсутствует система головного учета). Неизвестна суммарная нагрузка сети и при проектировании сети – ее получают в процессе расчета как сумму нагрузок узлов и потерь в сети. В этом случае балансировать узловые нагрузки не с чем и формула для погрешности в потерях мощности имеет вид:

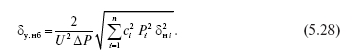
Примеры расчета погрешностей расчета потерь электроэнергии, обусловленных погрешностями данных об узловых нагрузках, приведены в прил. 4. Из известных программ их расчет для конкретной сети реализован только в программах комплекса «РАП-стандарт».

Информационная погрешность расчета ? и kф 2 по приближенным формулам

Такую погрешность, обусловленную погрешностью используемого в расчете значения kз , определяют по формулам (прил.4):

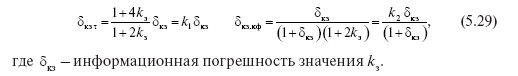
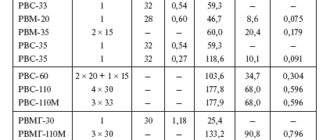
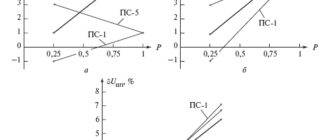
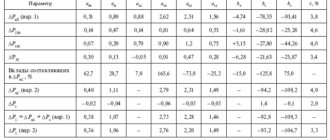
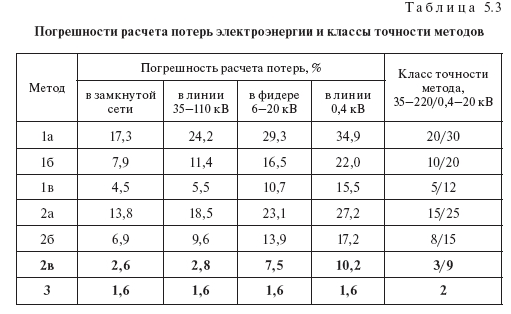
В табл. 5.3 приведены результаты расчета суммарных погрешностей методов 1–3 для сетей различных номинальных напряжений при погрешностях в нагрузках узлов ?н = ±10 %, в коэффициенте заполнения графика ?кз = ±10 % (погрешности обозначены ?? и ?к ф ), а также погрешности методов 1 и 2 при использовании ? и 2 ф k , 170 определенных непосредственно по графикам нагрузки по формулам (2.4) и (2.5); последние обозначены ?? гр и ?кф гр. Эти погрешности соответствуют расчетам по известной схеме сети. Буквой «а» обозначены методы, использующие приближенные формулы (2.16) и (2.17) для определения ? и 2 ф k и не использующие корректирующие коэффициенты kP, определяемые по формулам (2.30) – (2.32); буквой «б» – методы, использующие точные формулы (2.4) и (2.5) для определения ? и 2 ф k , но не использующие корректирующие коэффициенты kP ; буквой «в» – методы, использующие точные формулы (2.4) и (2.5) для определения ? и 2 ф k и корректирующие коэффициенты kP . В табл. 5.3 приведены также классы точности методов, представляющие собой их обобщенные характеристики, которые можно использовать для идентификации методов. Они установлены в виде двух цифр: для сетей 35–220 кВ и для сетей 0,4–20 кВ (в таблице приведены через дробь).

Данные табл. 5.3 показывают, что точность расчетов потерь существенно повышается, если использовать для определения ? и 2 ф k точные формулы (2.4) и (2.5) и применять корректирующие коэффициенты kP . В этом случае приемлемую точность показывает даже метод 1. Характеристики рекомендуемых методов выделены в таблице полужирным шрифтом.

Погрешности расчета нагрузочных потерь в одном элементе (токоограничивающий реактор, трансформатор СН подстанции и т. п.) включают в себя лишь две составляющие – методическую и информационную погрешность расчета ? или 2 ф k по приближенным формулам.

Таблица 5.3

Погрешности расчета потерь электроэнергии и классы точности методов

 Погрешности расчета потерь электроэнергии в сетях 0,4 кВ по обобщенным данным о схемах

В связи с обилием допущений, принятых при выводе формул (2.53) – (2.57), осуществить фрагментарный учет влияния каждого допущения трудно. В формировании суммарной погрешности участвуют все погрешности, учтенные в табл. 5.3, и, кроме того, погрешности в величинах k0,4, tg? и (1 – dн )2 . Если же оценить погрешность в k0,4 на уровне 20 %, а в остальных двух величинах на уровне 10 %, то суммарная погрешность расчета потерь в одной линии по формулам (2.53) – (2.57) составит 37 % (класс точности 40).

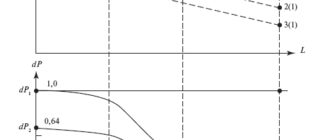
Погрешность расчета потерь по измеренным потерям напряжения ?U%, даже при реальном проведении натурных измерений, не может быть меньше. В ее формировании участвуют все погрешности, перечисленные выше, кроме погрешностей в величинах k0,4 и tg? (значение ?U% учитывает влияние на режим tg?). Однако прибавляется погрешность в величине ?U%.. Она определяется классами точности приборов, используемых при измерениях, возможными разнонаправленными погрешностями приборов в начале и конце линии, трудностями одновременного снятия их показаний, случайными колебаниями нагрузки в течение измерений и т. п. Например, зафиксированное при измерениях значение ?U% (при классах точности приборов 1,0) в действительности может соответствовать любому значению в диапазоне (?U% ± 2 %), то есть при измеренном ?U% = 8 % действительные потери напряжения могут быть и 6 %, и 10 %, что соответствует погрешности ±25 %. Поэтому класс точности этого метода также можно принять равным 40.