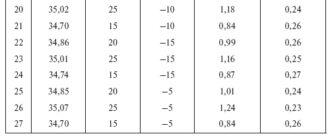
Электрические сети 0,4 кВ представляют собой, как правило, радиальные линии, связывающие шины 0,4 кВ РТ 6–20/0,4 кВ с вводными устройствами зданий. Сети 0,4 кВ крупных городов выполняются преимущественно кабельными линиями, а небольших городов и сельских населенных пунктов – воздушными.
На балансе сетевой организации обычно находится большое количество линий 0,4 кВ. Данные о схемах и нагрузках этих линий (особенно в сельской местности) либо отсутствуют, либо из-за их большого объема не могут быть достаточно быстро обработаны и введены в компьютер. Располагаемой информацией о схемах этих линий являются суммарная длина и количество линий с разными сечениями головных участков и суммарная электроэнергия, отпускаемая в эти линии.
Расчет потерь на основе обобщенных данных о схемах линий
Очевидно, что суммарной длины линий недостаточно для определения потерь электроэнергии, так как их значение существенно зависит от распределения нагрузок по линиям и разветвленности схем электрических сетей. В связи с этим возникает необходимость охарактеризовать схемы сетей какими-либо количественными показателями, более или менее легко определяемыми на основе объективных данных, а затем вывести зависимости потерь от этих показателей. Ниже рассмотрены способы учета при расчете потерь электроэнергии в сетях 0,38 кВ следующих влияющих факторов:
- характера распределения нагрузок по длине линии, отражаемого коэффициентом kр ;
- неодинаковости длин линий (их разброса относительно Lср), отражаемой коэффициентом kl ;
- неодинаковости плотности тока на головных участках линий (непропорциональности распределения суммарной энергии по линиям), отражаемой коэффициентом kj ;
- неодинаковости нагрузок фаз (несимметрии токов), отражаемой коэффициентом kнн;
- разветвленности схем сетей, отражаемой соотношением длины магистрали LМ и ответвлений (двух- или трехфазных L2–3 и однофазных L1 ). При этом под магистралью понимается наибольшее расстояние от шин ТП до последнего здания, получающего питание от трехфазной линии или от двухфазного ответвления (далее будет показано, что потери в трехфазной и двухфазной линиях одинаковы).
Учет характера распределения нагрузок по длине линии
Исходное выражение для нагрузочных потерь электроэнергии в линии с одинаковыми нагрузками фаз имеет вид:

Эквивалентное сопротивление зависит от конфигурации линии и распределения нагрузок по ее длине. Очевидно, что для линии, выполненной по всей длине проводом одного сечения, с нагрузкой, сосредоточенной в ее конце, Rэкв = r0 L , где r0 – удельное сопротивление провода, Ом/км, а L – длина линии, км, то есть Rэкв соответствует физическому сопротивлению линии.
Для такой же линии с нагрузкой, равномерно распределенной по ее длине, Rэкв определим из уравнения

Из этого следует, что при одинаковых длинах линий и сечениях проводов потери в линии с равномерно распределенной нагрузкой в 3 раза меньше, чем в линии с сосредоточенной нагрузкой. Если характеризовать влияние на потери мощности в линии характера распределения нагрузок по ее длине коэффициентом kр , то его значение при принятых выше условиях равно 0,33.
При уменьшении сечения линии по мере удаления от ТП пропорционально уменьшению нагрузки (линия с постоянной плотно- 370 стью тока) в (П3.2) необходимо вместо r0 перед знаком интеграла внести в подынтегральную функцию выражение

В результате интегрирования получим Rэкв = r0 L/2. Этот результат показывает, что потери в линии с равномерно распределенной нагрузкой в 2 раза меньше, чем в линии с сосредоточенной нагрузкой, то есть kр = 0,5.
Для идеализированной линии с n одинаковыми нагрузками, присоединенными на одинаковом расстоянии друг от друга, эквивалентное сопротивление определяется по формуле
![]()
При n = 1 (нагрузка сосредоточена в конце линии) Rэкв = r 0 L , а при увеличении n значение Rэкв приближается к r0 L/3.
На практике всю линию или ее магистральную часть выполняют проводом одного сечения и лишь в конце линии и на ответвлениях от нее могут использоваться провода меньшего сечения. Расчеты 144 реальных схем линий без ответвлений и с распределенными по длине линии нагрузками показали, что значения kр находятся в пределах 0,37 ± 0,04.
Линии, питающие жилую застройку, можно считать линиями с равномерно распределенной нагрузкой, особенно в сельской местности, где к линии, идущей вдоль улицы, через приблизительно одинаковые расстояния подключены жилые дома с приблизительно одинаковым уровнем электропотребления. Производственные предприятия сельской местности (животноводческие, зернообрабатывающие и др.) находятся обычно в стороне от жилых зданий, и к ним идут отдельные линии, которые можно считать линиями с сосредоточенной нагрузкой. Для таких линий kр =1.
Общая формула для определения kр имеет вид:
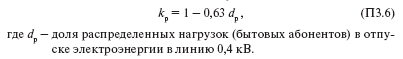
В диапазоне сечений алюминиевых проводов 25–70 мм2 , обычно используемых на ВЛ 0,4 кВ, справедливо соотношение r0 ? 28,5/F, где F – сечение провода. Подставляя в формулу (П3.1) U = 0,4 кВ и Rэк = r0 L = 28,5 kр L /F , получим:

Введем коэффициент k1 , отражающий характер распределения нагрузок по длине линии и по фазам:
![]()
и коэффициент k2 , отражающий неодинаковость длин линий и непропорциональность распределения суммарной нагрузки сети 0,4 кВ между линиями
![]()
Коэффициент k1 используется при расчете потерь в одной линии по ее индивидуальным характеристикам, а коэффициент k2 вводится в формулу дополнительно при расчете потерь в совокупности линий по их суммарным характеристикам (при расчете потерь в одной линии k2 = 1).
Формула (П3.7) при подстановке в нее указанных коэффициентов, среднего отпуска энергии в линию Wср = W? /N и суммарной длины всех участков L? (под линией понимается присоединение к шинам 0,4 кВ ТП 6–20/0,4 кВ) приобретет вид:

Учет неодинаковости длин линий
Влияние этого фактора рассмотрим на примере двух линий с сечениями F1 и F2 и длинами l 1 и l 2 . Суммарные потери в этих линиях при одинаковой плотности тока и учете их фактических длин
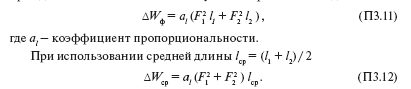
Отношение потерь при учете фактических длин линий к потерям при использовании средней длины
![]()
Обозначая среднеарифметическое отклонение длин линий от их среднего значения через ?l и предполагая, что линия с сечением провода F1 имеет длину меньше средней, а F2 – больше средней, получим:
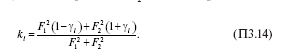
Значение этого коэффициента зависит от корреляции сечений головных участков и длин линий. Например, при F1 = 16 мм2 , F2 = = 25 мм2 (что соответствует предположению, что при малых сечениях головного участка длины линий в среднем меньше) и ?l = 0,3 значение kl = 1,13. Если же принять F1 = 25 мм2 , а F2 = 16 мм2 (менее реальное предположение, что длины линий меньше при больших 2 сечениях головных участков), то kl = 0,87.
Значение kl может быть с достаточной точностью вычислено по формуле, аппроксимирующей выражение (П3.14):

При первом предположении rF, l = 1 и по формуле (П3.15) kl = 1,14, а при втором предположении rF, l = –1 и kl = 0,86. Анализ реальных схем линий 0,4 кВ показал, что для линий, питающих сосредоточенные нагрузки, rF, l ? 0 и kl = 1. Для линий, питающих распределенные нагрузки, rF, l = 0,8 и kl = 1,11. В связи с этим для смешанной нагрузки
![]()
Учет неодинаковой плотности тока на головных участках различных линий
Так как в большинстве случаев данных об отпуске энергии в каждую линию нет, суммарный отпуск энергии в сеть 0,4 кВ обычно распределяют между линиями пропорционально сечениям головных участков. Статистический анализ более 1000 линий 0,4 кВ показал, что среднеарифметическое значение разброса плотностей тока составляет около 50 % их среднего значения, в связи с чем расчетное значение коэффициента kj может быть принято равным

Учет несимметрии нагрузок фаз
Коэффициент увеличения потерь в линии с несимметричной нагрузкой фаз определяют по формуле
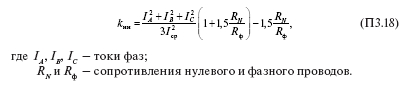
На практике измерить токи фаз во всех линиях 0,4 кВ, находящихся на балансе сетевой организации, трудно, поэтому в практических расчетах целесообразно использовать средние значения коэффициента kнн. При относительном отклонении токов фаз от их среднего значения в диапазоне 0,3–0,5 и отношения RN /Rф в диапазоне 1–1,5, коэффициент kнн изменяется в диапазоне от 1,15 до 1,55 (kнн = 1,35 ± 0,2). Это значение коэффициента может быть применено к линиям с распределенной нагрузкой, представляющей собой нагрузку жилых зданий, преимущественно однофазную. Сосредоточенные нагрузки имеют, как правило, большую долю симметричных, трехфазных нагрузок, поэтому kнн для таких линий находится в диапазоне 1,05 ± 0,05. Общая формула для коэффициента kнн имеет вид:
![]()
С учетом изложенного формулы для расчета коэффициентов k1 и k2 будут иметь вид:
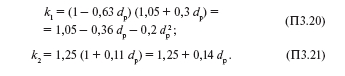
Учет разветвленности линий
При симметрии токов в фазах трехфазной сети ток в нулевом проводе отсутствует, а токи в фазных проводах одинаковы. В двухфазном ответвлении ток в обратном проводе с учетом фазового сдвига токов в проводах на 120° равен току фазного провода. В обоих случаях одинаковые токи текут по трем проводам, поэтому потери в трехфазном и двухфазном участках одинаковы. В однофазном же ответвлении одинаковый ток течет по двум проводам – фазному и нулевому, в связи с чем потери составляют 2/3 потерь в трехфазном участке такой же длины.
Коэффициенты приведения длин двухфазных и однофазных ответвлений к длине трехфазного участка могут быть получены для типовых схем распределения суммарной нагрузки между ответвлениями. Анализ многочисленных схем линий 0,4 кВ показал, что обычно число неполнофазных ответвлений от линии составляет либо три однофазных, либо одно двухфазное и одно однофазное (что обусловлено необходимостью равномерного распределения нагрузки между фазами).
Ток в проводе каждого из трех однофазных ответвлений составляет 1/3 суммарного тока трех фаз трехфазного участка, а потери – 374 1/9 потерь в трехфазном участке. Ввиду протекания того же тока в обратном проводе потери становятся равными 2/9 потерь в трехфазном участке. В связи с этим коэффициент приведения длины однофазных ответвлений к эквивалентной длине трехфазного участка составляет 2/9 = 0,22. В двухфазном ответвления суммарный ток в фазах составляет 2/3 суммы токов трехфазного участка, а потери – 4/9, что соответствует коэффициенту приведения 0,44. В соответствии с полученными соотношениями эквивалентную длину линии 0,4 кВ определяют по формуле (2.54).
Данная формула применима к наиболее широко распространенным проводам из алюминия. В ряде случаев некоторые участки линии могут быть проложены стальными или медными проводами. Сопротивление стального провода в среднем в 4 раза больше, чем алюминиевого провода такого же сечения, а сопротивление медного провода составляет 0,6 сопротивления алюминиевого, поэтому при их наличии в магистрали или ответвлениях в формулу (2.54) подставляют длины, определяемые по формуле (2.55).
Формула (П3.10) выведена в предположении о распределении суммарной энергии между нагрузками, расположенными по длине линии и сосредоточенными в ее конце. В действительности часть энергии потребляется непосредственно с шин 0,4 кВ ТП или на незначительном расстоянии от него («беспотерьное» потребление). Например, в сельской местности ТП обычно проектировались рядом с относительно крупными потребителями – домами культуры, магазинами и т. п. Долю «беспотерьного» потребления энергии dн можно принять близкой к доле коммунальных нагрузок (без бытовых абонентов). С учетом этого формула для расчета потерь электроэнергии в N линиях приобретет вид:
![]()
Обозначая произведение 7,42 k1 k2 через коэффициент k0,4 , получим окончательную формулу (2.53).
С учетом формулы (П3.20) коэффициент k0,4 при расчете потерь электроэнергии в одной линии (k2 = 1) определяют по формуле (2.56), а в совокупности линий (k2 = 1,25 + 0,14 dр ) – по формуле (2.57).
Все приведенные формулы соответствуют сетям напряжением 400/230 В. В некоторых регионах сохранились старые сети с напряжением 220/127 В. Для расчета потерь в таких сетях в формулы вводится коэффициент 3.
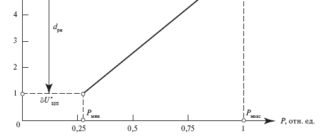
Расчет потерь электроэнергии на основе измеренных максимальных потерь напряжения в линии
Для линии с сосредоточенной в конце нагрузкой и сопротивлением R + jX относительные потери мощности и напряжения в максимум нагрузки выражаются формулами:

Для ВЛ x0 ? 0,4 Ом/км, а r0 ? 28,5/Fг , где Fг – сечение провода головного участка, ? = F / 71. Учитывая уменьшение сечения проводов по мере удаления от ТП (особенно на ответвлении, в удаленной точке которого и проводят измерения напряжения), эквивалентное значение ? снижается. Для практических расчетов примем ? = Fг /100. При этом формула для коэффициента kм/н будет иметь вид:
![]()
Для кабельных линий ? = 0 и kм/н = 1 + tg2 ?.
Для линии с равномерно распределенной нагрузкой

Разделив (П2.28) на (П2.29) и учитывая принятое значение ? = = Fг /100, получим:
![]()
Значение дроби 2/3 соответствует равномерному распределению нагрузки вдоль линии.
В соответствии с (П3.5) потери мощности в идеализированной линии с n одинаковыми нагрузками, присоединенными на одинаковом расстоянии друг от друга, уменьшаются по сравнению с потерями мощности в линии с нагрузкой, сосредоточенной в конце в (n + 1) (2n + 1) / 6n2 раз (при росте n эта величина стремится к значению 1/3).
Потери напряжения в такой линии определяются по формуле

Из формулы (П3.31) следует, что потери напряжения в линии с n одинаковыми нагрузками по сравнению с линией, нагрузка которой сосредоточена в конце, уменьшаются в (n + 1) / 2n раз. При росте n эта величина стремится к значению 1/2, то есть при равномерно распределенной нагрузке потери напряжения уменьшаются в 2 раза. Коэффициент 2/3 в формуле (П3.30) является предельным соотношением величин (n + 1) (2n + 1) / 6n2 и (n + 1) / 2n, равным (2n + 1) / 3n. Например, при n = 10 значение (2n + 1) / 3n = 0,7.
Следует отметить, что соотношения (П3.5) и (П3.31) выведены для идеализированной линии, представляющей собой магистраль без ответвлений. Иногда в публикациях встречаются попытки типизировать схемы линий 0,4 кВ, представив несколько идеализированных схем с различной конфигурацией, для которых вычисляют данный коэффициент.
Любая реальная линия отличается от идеализированных типовых схем: длины участков в реальных линиях неодинаковы, ответвления в некоторых узлах могут отсутствовать, а в других они могут иметь другие длины и т. п. Попытки поставить конкретную схему в соответствие с определенным типом идеализированной схемы приводят к большим затратам труда, чем ввод схемы реальной линии 2 в компьютер для проведения точного расчета. Рассмотрение конкретных схем тем более затруднено, когда речь идет об оценке суммарных потерь во всех линиях 0,4 кВ, находящихся на балансе сетевой организации.
Для практических расчетов можно принять значение этого коэффициента для линий с распределенной нагрузкой равным 0,75. Общая формула для любого распределения нагрузки имеет вид:
![]()
Переходя от потерь мощности к потерям электроэнергии и обозначая произведение коэффициента kм/н на коэффициент kэ/м (2.49) через kэ/н и учитывая коэффициент несимметрии kнн, получим окончательную формулу для расчета относительных потерь электроэнергии:
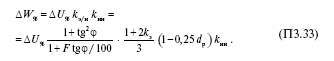

 onetwoclick.ru
onetwoclick.ru