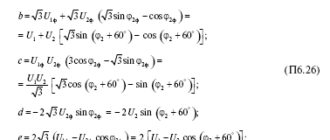Определение симметричных составляющих в фазных и междуфазных напряжений: расчет, формулы

Обратная последовательность

На рис. П6.1 изображены в виде звезды системы векторов междуфазных напряжений UАВ, UВC, UCA и напряжений прямой UАВ (1), UВC (1), UCA (1) и обратной UАВ (2), UВC (2), UCA (2) последовательностей. За действительную ось принят вектор UАВ (1). Вектор UАВ (2) сдвинут относительно вектора UАВ (2) на угол ?2 . Вектора UВC (2) и UCA (2) сдвинуты относительно векторов UВC (1) и UCA (1) на углы ?2 – 120° и ?2 + 120° соответственно.

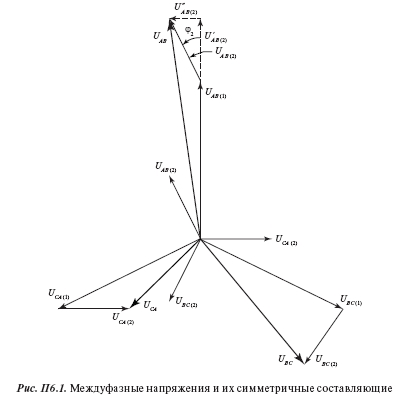
Рис. П6.1. Междуфазные напряжения и их симметричные составляющие

Связь модулей междуфазных напряжений UАВ != UВC != UCA и модулей напряжений прямой U1 = UАВ (1) = UВC (1) = UCA (1) и обратной U2 = = UАВ (2) = UВC (2) = UCA (2) последовательностей выражается системой трех уравнений, содержащих три неизвестных – U1 , U2 и ?2 :

Возводя каждое уравнение системы (П6.1) в квадрат и используя тригонометрические формулы для косинусов и синусов сумм и разностей аргументов:

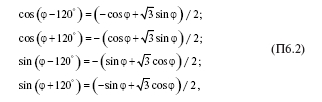
получим систему уравнений:

Для исключения величин U1 2 и U2 2 вычтем третье уравнение из первого и второго уравнения и получим систему двух уравнений:

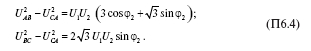
Определяя из каждого уравнения (П6.4) величину U2 и приравнивая полученные выражения, получим:

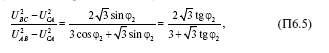
откуда непосредственно следует:

Если знаменатель формулы (П6.6) меньше нуля, к углу ?2 надо прибавить 180°.

Для упрощения записи последующих уравнений введем следующие обозначения:

 

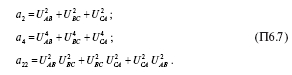
Из соотношения тригонометрических функций и с учетом принятых обозначений имеем:

Из второго уравнения (П6.4) имеем:

Подставив (П6.9) в первое уравнение (П6.4), получим выражение для cos ?2 через другие величины:

Приравнивая (П6.8) и (П6.10), получим связь величин U1 и U2 :

Подставив (П6.8) и второе уравнение (П6.11) в первое уравнение системы (П6.3), получим биквадратное уравнение:

решение которого дает окончательную формулу:

Если подставить в (П6.3) не второе, а первое уравнение (П6.11), то получим формулу для U2 , правая часть которой полностью совпадает с (П6.13). Это не удивительно, так как формулы (П6.3) инвариантны по отношению к величинам U1 и U2 : при одновременной замене U1 на U2 и U2 на U1 формулы не изменяются. Поэтому при знаке «+» перед внутренним корнем в формуле (П6.13) по ней 402 определяется величина, имеющая большее значение, а при знаке «–» – меньшее. Так как физически U1 > U2 , то общая формула имеет вид (8.6). Данные формулы были впервые выведены в 1985 г. [44].

Для проверки правильности полученных формул примем в качестве примера значения междуфазных напряжений, соответствующие U1 = 400 В; U2 = 40 В и ?2 = 30°. Подставив эти значения в формулы (П6.1), получим: UAB = 435,1 В; UBC = 402,0 В; UCA = 365,9 В.

Приняв эти напряжения в качестве исходных данных, по формулам (8.6) и (8.7) получим: U1 = 400 В; U2 = 40 В; ? 2 = 30° , что говорит о правильности формул.

Преобразования уравнений (П6.1) могут проводиться различными способами. Например, в [45] приведена формула для напряжения обратной последовательности, также использующая величины (П6.7) и определяющая значение U2 в процентах от U1 (формула для U1 в [45] не приведена, поэтому значение U2 в вольтах оказывается не определенным):

 

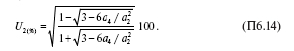
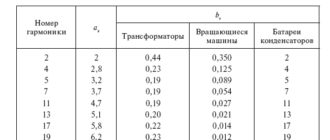
Подставив в формулу значения a4 и a2 , получим U2 (%) = 10 %.

Нулевая последовательность

В фазных напряжениях содержатся все три последовательности. Система уравнений, связывающая модули фазных напряжений с модулями напряжений прямой, обратной и нулевой последовательности, имеет вид:

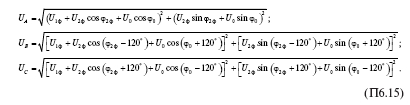
В уравнениях (П6.15) пять неизвестных: U1ф, U2ф, U0 , ?2ф и ?0 . Получить выражения для них из системы трех уравнений невозможно. Поэтому рассчитать составляющие прямой, обратной и нулевой последовательностей фазных напряжений на основании измерения только фазных напряжений нельзя. Необходимо использовать полученные из расчета междуфазных напряжений составляющие прямой и обратной последовательности фазных напряжений: U1ф = = U1 / 3 и U2ф = U2 / 3 . Угол ? 2ф между U2ф и U1ф связан с углом 403 между U2 и U1 . соотношением ? 2ф = ? 2 + 60°, то есть также является известным. При этом в (П6.15) остается только два неизвестных: U0 и ? 0 . Система уравнений оказывается избыточной – достаточно использовать два любых уравнения. Тем не менее продолжим операции со всеми тремя уравнениями, так как вывод окончательных формул оказывается проще.

Для упрощения записи (П6.15) произведения и суммы уже известных величин и являющихся при выводе соотношений для U0 постоянными, обозначим:

Для упрощения дальнейших преобразований исключим величину U0 2 . Для этого вычтем из первого уравнения второе, а из второго третье уравнение и получим систему из двух уравнений:

Величины в круглых скобках формул (П6.20), являющиеся постоянными, для упрощения записи обозначим:

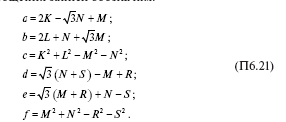
При этом формулы (П6.20) приобретут вид:

Выражая из каждого уравнения U0 и приравнивая правые части полученных формул, получим:

 

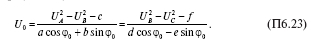
Равенство правых частей формулы (П6.23) запишем в виде:

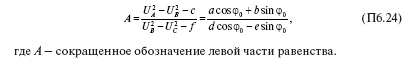
Разделив числитель и знаменатель правой части равенства на cos ?0 , получим:

После определения угла ?0 значение U0 определяют, подставляя его в любое из уравнений (П6.23).

Приведенный алгоритм вычисления предполагает определение U0 после предварительного определения ?0 . Подставив (П6.25) в соотношения

и затем в (П6.23), можно получить формулу, непосредственно определяющую U0 через фазные и междуфазные напряжения, однако она получается чрезмерно громоздкой. Поэтому целесообразнее использовать последовательно формулы (П6.25) и (П6.23).

Подставив в (П6.21) выражения (П6.16), получим формулы, непосредственно связывающие величины a, b, c, d, e, f с определенными на первом этапе параметрами прямой и обратной последовательности (как в фазных, так и в междуфазных напряжениях):

Для проверки правильности полученных формул примем в качестве примера значения фазных напряжений, соответствующие U0 = 20 В, ?0 = 60° и полученным ранее из расчета междуфазных напряжений U1ф = 400 / 3 , U2ф = 40 / 3 и ?2ф = ?2 + 60° = 30° + 60° = 90°. Подставив эти значения в формулы (П6.15), получим:

По (П6.26) вычисляем коэффициенты:

Подставив эти данные последовательно в (П6.24), (П6.25) и (П6.23), получим:

что подтверждает правильность расчетных формул.

Все приведенные выше формулы получены исходя из первоначальных систем уравнений, связывающих фазные и междуфазные напряжения с напряжениями симметричных составляющих и углами между ними. Другой способ вывода подобных формул основан на использовании соотношений между сторонами и углами косоугольных треугольников.

Известны формулы, выведенные Ф. Ф. Карповым (приведены в «Методических указаниях по контролю и анализу качества электроэнергии в электрических сетях общего назначения», опубликованных в [46]), в соответствии с которыми параметры напряжения прямой и обратной последовательности определяют следующим образом:

где U? и U? с соответствующими нижними индексами – продольная и поперечная составляющие векторов U1 и U2 ; ?1(2)–AB – углы векторов U1 и U2 по отношению к вектору UBA. Если U? 1(2) < 0, к ?1–AB и ?2–AB надо прибавить 180°. Угол вектора U2 относительно вектора U1 определяется разностью ?2–1 = ?2–AB – ? 1–АB.

Для определения значений U? 1(2) и U? ? 1(2) вначале рассчитывают вспомогательные величины:

а затем подставляют их в формулы:

В формулах (П6.29) при определении составляющих вектора U1 принимают знак «+», а вектора U2 – знак «–». Значения прямой и обратной последовательности, определенные по этим выражениям для условий примера, полностью совпадают с определенными выше, при этом углы ?1–АB = –2°40?; ?2–AB = 27°20? и ?2 = ?2–AB – ?1–АB = 30°.

Параметры напряжения нулевой последовательности в соответствии с [46] определяют по формулам:

Для определения значений U? 0 и U? 0 дополнительно к величинам (П6.28) рассчитывают вспомогательные величины:

а затем подставляют все вспомогательные величины в формулы:

При преобразовании соотношений между сторонами и углами косоугольных треугольников могут использоваться различные приемы. Полученные при этом расчетные формулы могут иметь различный внешний вид, однако если при их выводе не использовались допущения (например, пренебрежение какими-либо составляющими вследствие их заведомой малости по сравнению с остальными), то все формулы дают идентичные результаты.

В частности, в ГОСТ 13109–97 [47] приведены формулы (в формуле для U0 исправлены знаки перед X и Y):

К сожалению, к этим относительно простым по виду выражениям нет формул для определения углов между векторами симметричных составляющих. Для целей сопоставления рассчитанных величин с нормами стандарта углы не нужны, однако при выборе средств симметрирования режима (например, расчета мощности конденсаторов по фазам) без них обойтись нельзя.

Все приведенные выше формулы являются точными алгебраическими выражениями, дающими абсолютно идентичные результаты. При экспресс-оценке симметричных составляющих по результатам измерения без применения сложных формул можно использовать приближенные соотношения:

При различных значениях угла ?2 коэффициент во второй формуле не выходит за пределы 0,575–0,665, поэтому максимальная погрешность приближенного определения U2 не превышает 7,3 %. Погрешность приближенного определения U1 еще меньше, причем среднее значение междуфазных напряжений всегда несколько больше фактического значения U1 . Это превышение зависит от значения U2 и хорошо аппроксимируется формулой ?U1 (%) = 0,0025 U2 (%) 2 . Например, при U2 = 2 % превышение составит всего 0,01 %, а при U2 = 10 % – 0,25 %.

Для приведенного примера по формулам (П6.35) получаем: U1 = = 401 В и U2 = 42,9 В (U2 (%) = 10,7 %). Если уточнить значение U1 вычитанием превышения ?U1 = 0,0025 • 10,72 • 401 = 1,15 В, то U1 = 399,85 В, то есть U1 определяется с погрешностью менее 0,04 %.

Балансировка фазных и междуфазных напряжений

Необходимость такой балансировки обоснована в п. 8.1.2. Вид уравнений корректировки измеренных напряжений с целью приведения их к физически существующей системе зависит от принятого критерия балансировки. Возможны следующие критерии.

1. Оставить пять напряжений неизменными, а последнее фазное напряжение изменить так, чтобы оно пришло в нулевую точку, определенную двумя другими фазными напряжениями (см. рис. 8.4, в). Обоснованность такого подхода сомнительна, так как неясно, по какому условию должно выбираться единственное «неточное» напряжение, требующее корректировки.
2. Осуществлять корректировку всех фазных напряжений, оставив неизменными междуфазные напряжения. В этом случае встает вопрос, почему междуфазные напряжения следует считать точными, а фазные – неточными?
3. Так как все шесть напряжений измерены с погрешностью, представляется более логичным, что все они должны быть подвергнуты корректировке. При этом направленность корректировки фазных 409 и междуфазных напряжений оказывается различной. В случае, изображенном на рис. 8.4, а, междуфазные напряжения должны быть несколько увеличены, а фазные уменьшены, а в случае, изображенном на рис. 8.4, б, – наоборот. Считая, что все напряжения измерены прибором с одинаковой относительной погрешностью ?, представляется логичным, что все шесть напряжений должны быть изменены в одинаковой пропорции (хотя и в разные стороны). При таком подходе встает вопрос: почему предполагается, что при измерении всех междуфазных напряжений погрешность проявилась в одну сторону, а при измерении всех фазных напряжений – в другую?

К каждому из подходов имеются вопросы, которые, как кажется, полностью демонстрируют нелогичность рассмотренных подходов. Тем не менее задача состоит не в опровержении подходов, а в предложении хотя бы одного приемлемого, так как проводить расчеты симметричных составляющих для физически несуществующей системы исходных векторов еще более нелогично.

Условием физического существования системы является равенство ?АВ + ?ВС + ?СА = 360° (на рис. 8.4, а сумма фактических углов больше 360°, а на рис. 8.4, б – меньше 360°).

Из известных соотношений сторон и углов косоугольных треугольников угол ?АВ определяется по формуле

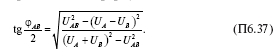
Аналогичные выражения могут быть записаны и для углов ?ВС и ?СА . Сумма половинных углов, естественно, должна быть равна 180°. Определенная же по измеренным напряжениям, она всегда будет отличаться от этой величины. Степень отличия охарактеризуем соотношением:

Значения напряжений в формуле (П6.37) необходимо скорректировать таким образом, чтобы определенные по (П6.37) углы удовлетворяли условию k? = 1. Это условие может быть обеспечено при различном изменении углов, входящих в сумму. Критерий корректировки углов неочевиден: корректировать ли все углы в одинаковой степени или в большей пропорции изменять меньшие углы (или наоборот)? Из описанных выше подходов наименьшие недостатки присущи третьему. Выведем соотношения для корректировки напряжений исходя из этого подхода и условия корректировки всех углов в одинаковой степени: к / i i k ? =? ? .

Для того, чтобы угол ?АВ, определяемый по формуле (П6.37), стал равным к ?AB , необходимо изменить напряжения UAB, UA, UB в соответствии с равенством

Аналогичные коэффициенты могут быть определены и для двух других треугольников. Коэффициенты будут отличаться друг от друга, что объясняется принятым допущением о корректировке всех углов в одинаковой пропорции. Вместе с тем в каждом треугольнике две стороны являются общими для смежных треугольников и не могут корректироваться по-разному. Единственным видимым выходом является применение ко всем напряжениям среднего коэффициента корректировки kU = (kU AB + kU BC + kU CA ) / 3.

Для примера предположим, что в результате измерений получены следующие напряжения:

Вычислив по формуле (П6.37) и подобным формулам для других треугольников соответствующие углы, получим:

Сумма углов составляет 196,2°, то есть система соответствует случаю рис. 8.4, б. Необходимо уменьшить углы, разделив их на коэффициент k? = 196,2 / 180 = 1,09. При этом значения углов к / 2 ?AB и соответствующих им тангенсов составят:

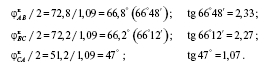
Подставляя эти значения tg ? в формулу (П6.40) и в подобные формулы, записанные для других междуфазных и фазных напряжений, получим:

Применив kU ср к измеренным напряжениям, получим:

Если определить по формулам типа (П6.37) углы для этой системы напряжений, то их сумма составит (65,1° + 64,8° + 48,3°) = = 178,2°, то есть вместо превышения на 16,2° сумма стала ниже необходимой на 1,8°. При желании можно сделать еще одну итерацию.

Для получения формулы корректировки напряжений для случая, когда начальная сумма углов оказывается меньше 180° (рис. 8.4, а), необходимо в формуле (П6.39) заменить деление на kU умножением, и наоборот. Однако, в связи с небольшим отличием значений kU от единицы, результат будет отличаться несущественно. Поэтому и в этом случае можно пользоваться формулой (П6.40); при этом значения kU окажутся чуть меньше единицы и приведут к необходимому увеличению междуфазных и уменьшению фазных напряжений.

При использовании приведенного алгоритма поставленная цель – создание физически существующей системы векторов – достигается. Однако остаются вопросы об обоснованности принятого критерия – изменение фазных и междуфазных напряжений в разные стороны. Учитывая случайный характер измеренных величин, представляется наиболее обоснованным использовать критерий минимума суммы квадратов отклонений относительных значений скорректированных напряжений от их измеренных значений:

при одновременном соблюдении условия, накладываемого на сумму углов. Решение такой системы уравнений в настоящее время отсутствует.

В целом алгоритм вычисления параметров симметричных составляющих состоит из следующих этапов:

• проводят балансировку фазных и междуфазных напряжений;
• вычисляют параметры прямой и обратной последовательности междуфазных напряжений по формулам (8.6) и (8.7) или другим аналогичным формулам;
• по формулам (8.8) вычисляют коэффициенты a, b, c, d, e, f; по формулам (8.9) – (8.11) вычисляют параметры нулевой последовательности.