Условие эквивалентности воздействия случайного процесса изменения параметра и постоянной, длительно допустимой величины в обозначениях теории вероятностей записывается следующим образом:
![]()
где символом M обозначено математическое ожидание функции.
Любое значение случайного процесса связано с его характеристиками соотношением:
![]()
Обозначая значение параметра ?i , соответствующее Хнорм, как ?экв и подставляя (П7.2) в (П7.1), получаем выражение:
![]()
из которого численное значение ?экв определяют путем подстановки развернутого выражения функции f (X) для конкретного оборудования.
Наиболее распространенным видом функции f (X) в энергетических задачах является степенная функция
![]()
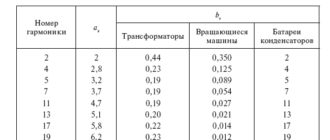
Например, нагрев оборудования пропорционален квадрату тока, срок службы ламп накаливания зависит от напряжения в 14 степени и т. п. В этом случае выражение (П7.3) приобретает вид:
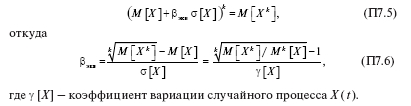
Математическое ожидание k-й степени случайной величины определяют по известной формуле:
![]()
где ? (X) – закон распределения значений случайного процесса X (t).
В дальнейшем для упрощения записи характеристики случайной величины X будем обозначать тх , ?x , и ? х.
Для нормального закона распределения
![]()
Производя замену переменной
![]()
и подставляя (П7.8) в (П7.7), получаем:
![]()
Используя формулу бинома Ньютона, приведем (П7.11) к сумме интегралов, каждый из которых в соответствии с рекуррентным соотношением
![]()
сводится при четном k к интегралу
![]()
а при нечетном k к интегралу
![]()
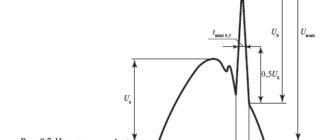
В результате слагаемые (П7.10), содержащие нечетные степени ?x , в окончательном выражении будут отсутствовать, а слагаемые с четными степенями ?x будут иметь сомножитель
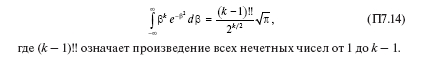
Подкоренное выражение (П7.6) приобретет вид:
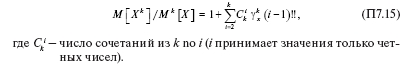
Например, при k = 7
![]()
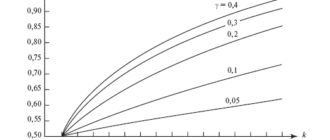
Зависимости ?экв = f ( k, ?х ), вычисленные по формуле (П7.6), приведены на рис. 8.9, а зависимости вероятности выхода случайного процесса за установленный предел, при которой его воздействие аналогично воздействию постоянной величины параметра, равной этому пределу (в случае нормального закона распределения) – на рис. 8.10. Результаты вычислений показывают, что допустимое значение вероятности выхода случайного процесса за установленный уровень зависит от характеристик процесса и не может быть нормировано однозначно. Значение вероятности, равное 0,95, является завышенным даже для ламп накаливания (k = 14).
Выражение (П7.3) справедливо для любого вида функции f (X). В практически важном случае линейно-квадратичной зависимости
![]()
выражение (П7.3) имеет вид квадратного уравнения
![]()
откуда ?экв получают как положительный корень уравнения
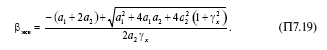

Милые киски встречаются с приятными мужчинами, проститутки в Липецке, для самого приятного времяпровождения. Определяйтесь по ценовым показателям, которые указаны в каждой анкете проститутки. Сексуальные проститутки в Липецке, восхитительные и горячие, они такие интересные и оригинальные, что интимный досуг тебе обеспечен. Выбери девушку сейчас.
 onetwoclick.ru
onetwoclick.ru