Сумматоры и цифровые компараторы: принцип работы, схемы

Что такое сумматоры?

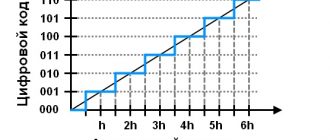
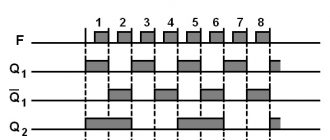
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел А и В, значение результата суммирования S и значение переноса в старший разряд P (см. рис. 3.48).

Цифровые сумматоры

Работа устройства, реализующего таблицу истинность (рис. 3.48), описывается следующими уравнениями

S = А·В + А·В

Р = А·В

Очевидно, что по отношении: к столбцу S реализуется логическая функция «исключающее ИЛИ», т. е. S = А + В.

Васильев Дмитрий Петрович

Профессор электротехники СПбГПУ

Задать вопрос

Устройство, реализующее таблицу (рис. 3.48), называют полусумматором, и оно имеет логическую структуру, изображенную на рис. 3.49.

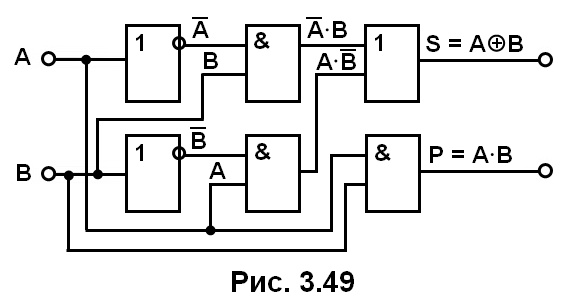
Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде.

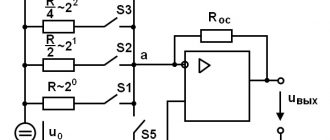
При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство (рис. 3.50) называют полным сумматором и его можно представить как объединение двух полусумматоров (Р_вх — дополнительный вход переноса).

Сумматор обозначают через SM.

Цифровые компараторы

Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном коде. Они могут определять равенство двух двоичных чисел A и B с одинаковым количеством разрядов либо вид неравенства A> B или A < B. Цифровые компараторы имеют три выхода.

Абрамян Евгений Павлович

Доцент кафедры электротехники СПбГПУ

Задать вопрос

Схема одноразрядного компаратора представляет собой структуру логического элемента «исключающее ИЛИ-НЕ» (рис. 3.51).

Из анализа схемы следует, что если A= B, то F = 1, в противном случае, т. е. при А != В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А < В, т. е. А = 0, В = 1, то D = l.

Если попарно равны между собой все разряды двух n-разрядных двоичных чисел, то равны и эти два числа А и В. Применяя цифровой компаратор для каждого разряда, например, четырехзначных чисел, и определяя значения F1, F2, F3, F4 логических переменных на выходах компараторов, факт равенства А = В установим в случае, когда F = F1 · F2 · F3 · F4 = 1. Если же F = 0, то А != В.

Неравенство А > В обеспечивается (для четырехразрядного числа) в четырех случаях: или А₄ > В₄, или А₄ = В₄ и А₃ > В₃, или А₄ = В₄, А₃ = В₃ и А₂ > В₂, или А₄ = В₄, А₃ = В₃, А₂ = В₂ и A₁ > В₁ (где А₄ и В₄ — старшие разряды чисел А и В). Очевидно, что если поменять местами А₁ и B₁, то будет выполняться неравенство А < В.

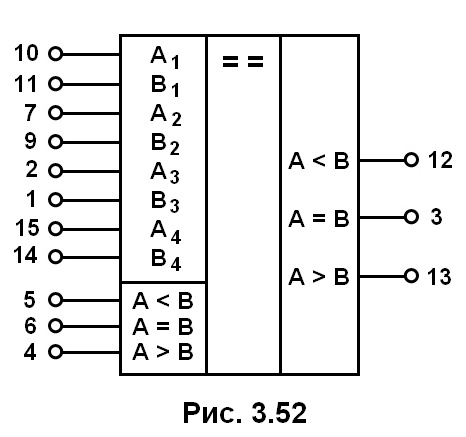
Цифровые компараторы выпускают, как правило, в виде самостоятельных микросхем. Так, микросхема К564ИП2 (рис. 3.52) является четырехразрядным компаратором, в котором каждый из одноразрядных компараторов аналогичен рассмотренной ранее схеме. Данная микросхема имеет расширяющие входы А < В, А = В, А > В, что позволяет наращивать разрядность обоих чисел. Для этого компараторы соединяют каскадно или параллельно (пирамидально).

Васильев Дмитрий Петрович

Профессор электротехники СПбГПУ

Задать вопрос

Рассмотрим каскадное соединение компараторов К564ИП2 для сравнения двух восьмиразрядных чисел (рис. 3.53). При этом соединении выходы А = В и А < В предыдущей микросхемы (младшие разряды) подключают к соответствующим входам последующей. На входы А < В, А = В, А > В микросхемы младших разрядов подают соответственно потенциалы U0 и U1 (U0 соответствует логическому 0, a U1 — «1»). В последующих микросхемах на входах А > В поддерживают потенциал логической единицы U1.